Normalverteilung - ja oder nein?
Hallo ihr Lieben,
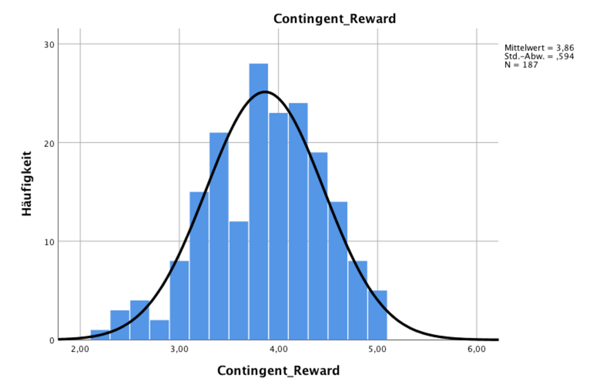
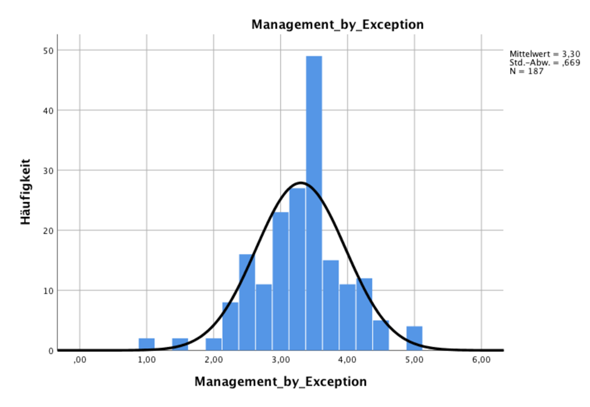
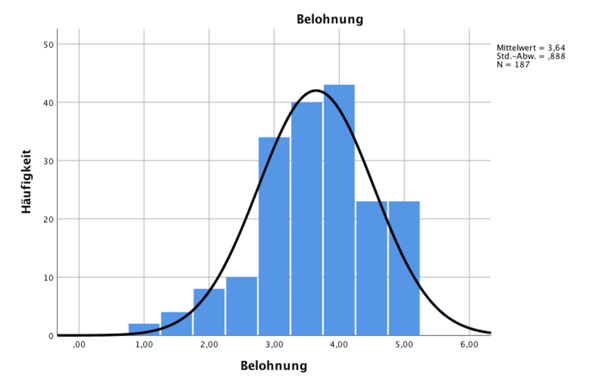
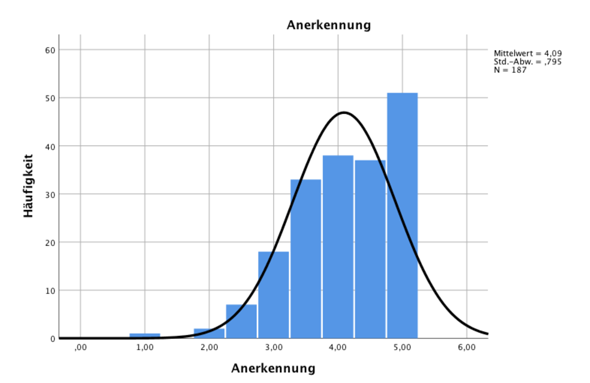
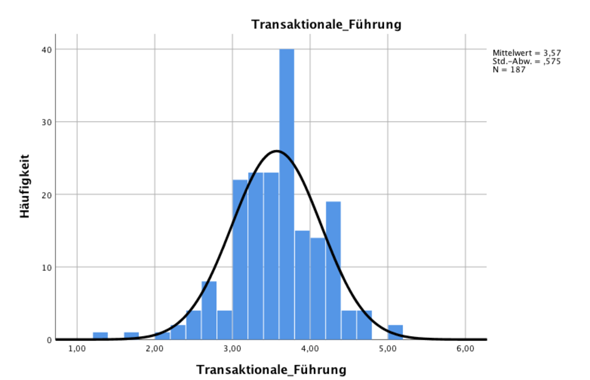
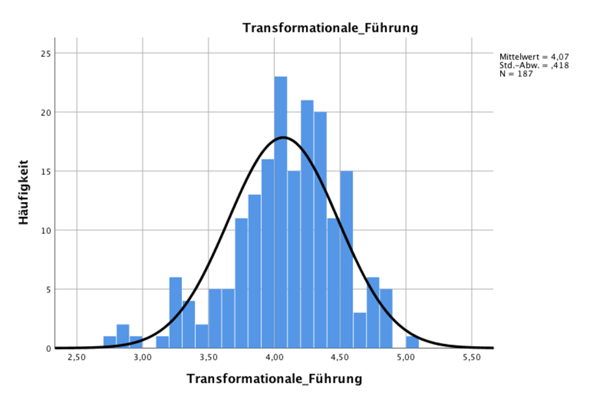
ich sitze momentan an der Auswertung meines Datensatzes für die Bachelorarbeit. Für die Durchführung eines t-tests möchte ich auf Normalverteilung schließen können. Der Shapiro-Wilk-Test führte zur Verwerfung der Nullhypothese und schließt damit nicht auf Normalverteilung. Laut verschiedenen Quellen ist der Shapiro-Wilk-Test bei größeren Datensätzen sensibler für minimale Abweichungen und führt damit schnell zur Ablehnung der Nullhypothese. Aus diesem Grund wird vorgeschlagen sich eher auf die Histogramme zu verlassen. Wenn ihr euch nun meine Histogramme anschaut, würden ihr mir zustimmen, dass man bis auf bei Belohnung und Anerkennung auf annähernde Normalverteilung schließen kann? Ich bin mir da irgendwie echt unschlüssig.
Liebe Grüße
2 Antworten
Für den t-Test ist es irrelevant, ob die Daten aus einer normalverteilten Grundgesamtheit stammen (und selbst wenn es relevant wäre, so sind statistische Signifikanztests zur Abtestung der Verteilungsvoraussetzung ein miserables, irreführendes Mittel, entweder zu sensitiv oder zu unsensitiv). Für den t-Test sollen die Daten innerhalb jeder Gruppe jeweils aus einer normalverteilten Grundgesamtheit stammen. Aber auch diese Annahme ist für die Zuverlässigkeit des t-Tests irrelevant, wenn die Stichprobe groß genug ist (zentraler Grenzwertsatz). n > 30 wird da als Voraussetzung oft genannt, Dein n=187 ist mehr als ausreichend, um sich um den Normalverteilungsquatsch nicht zu kümmern ("Normalverteilungsquatsch" deswegen, weil permanent die falsche Vorstellung "ich muss Normalverteilung haben für den t-Test" den Studenten Lebenszeit stiehlt und andere Annahmen immer weitaus relevanter sind als das).
In der Tat, Belohnung und Anerkennung wollen nicht so passen wie die anderen.
Deine Häufigkeiten (~200) lassen ggf hier auch nicht genügend Präzission zu.
Daher ggf noch über ein Maß für die Abweichung nachdenken, die eine Aussage auf Normalverteilung Gewicht verleit.
Wie meinst du das genau? :) Der Shapiro-Wilk und der Smirnov verwerfen ja leider beide die Nullhypothese
und für die anderen meinst du kann ich schon auf annähernde Normalverteilung schließen?