Mittelwert berechnen einer sinusförmigen Wechselspannung?
Hallo :) kann mir bitte bitte einer erklären wie ich hier den Mittelwert und den Effektivwert ausrechne. Verzweifel hier noch :(
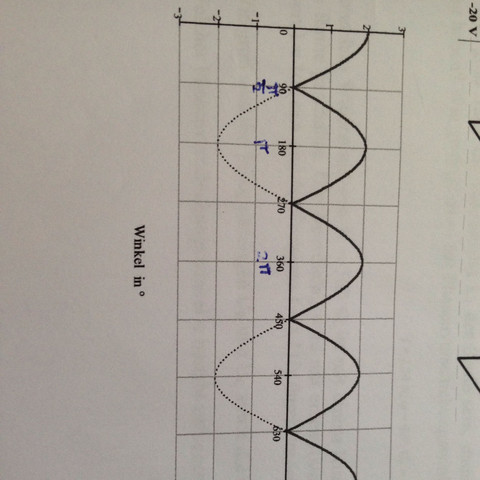
3 Antworten
Effektivwert:
Für die in T periodische Funktion
ist der Effektivwert
Du musst also über das Quadrat deines Cosinus integrieren. Das ist nicht schwer und man kann das Ergebnis auch schon durch Hinschauen sehen.
- dein Sinus ist komisch... sieht mehr aus wie Betrag von Cosinus...
- also der Mittelwert geht ja oft über das Integral... man könnte von 90° bis 180° integrieren... dann hat man die Fläche von einer halben Halbwelle... :)
- der Effektivwert ist das Integral vom Quadrat von u(t)...
- https://de.wikipedia.org/wiki/Effektivwert
Also bei Wiki steht: "Der Effektivwert entspricht mathematisch der Wurzel aus dem Mittelwert über das Quadrat der Spannungs- bzw. Stromfunktion während einer ganzen Zahl von Perioden."
--> als erstes musst Du also die Kurve quadrieren (sonst wäre der Mittelwert bei einer Wechselspannung ja auch genau 0)
--> dann bildest Du auf diese quadrierte Kurve (2 Perioden) den Mittelwert
--> dann zioehst Du die Wurzel davon
das ist der Effektivwert.
- ja, Wurzel vergessen... sowwy :)
- warum 2 Perioden? meinst 2 Höcker? warum nich nur n halben Höcker und dann mal 4?
Beim Sinus ist der Mittelwert 0 aber da du nur die positiven Halbweltergewicht hast, brauchst du die Kurvendiskussion. Den effektivere berechnest du mit: I eff=I spitze/Wurzel 2
Oder U eff=U Spitze/ Wurzel 2
Ja stimmt, es ist Cosinus! Aber trotzdem komm ich nicht auf das richtige weil die Aufleitung wär ja dann Sinus und dann kommt da null raus :(