Maxima und Minima abschätzen?
Hallo, ich schaue mir gerade eine Aufgabe zu Bestimmung der Lipschitzstetigkeits-Konstante L an.
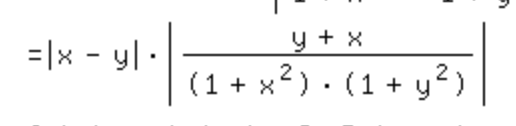
Ich weiß, dass ich an dem Punkt eigentlich bloß nach oben abschätzen muss. Mein Problem ist aber, dass der Definitions Bereich ganz |R ist. Wie gehe ich damit um?
2 Antworten
Ich würde da beispielsweise folgendermaßen abschätzen...
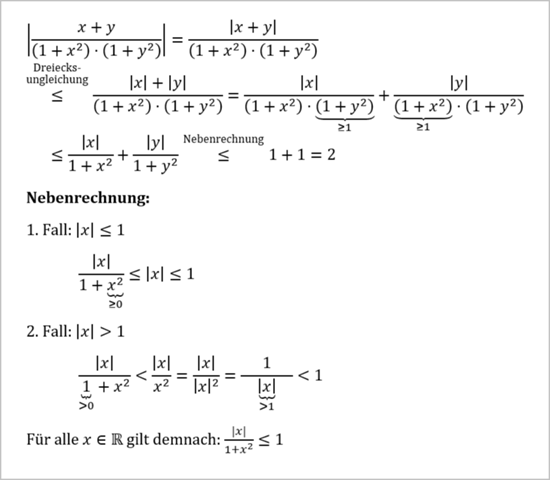
Eine Schwierigkeit besteht vielleicht darin zu erkennen, dass man bei den beiden Summanden (nach der Dreiecksungleichung) unterschiedlich abschätzen kann. Beim einen Summanden 1 + x² ≥ 1 und beim anderen Summanden 1 + y² ≥ 1.
Eine andere Schwierigkeit besteht vielleicht darin, zu erkennen, dass beim Abschätzen von |x|/(1 + x²) eine Fallunterscheidung [einmal für kleine Beträge von x und einmal für große Beträge von x] sinnvoll sein kann. Man könnte stattdessen aber auch die durch den Funktionsterm |x|/(1 + x²) gegebene reelle Funktion betrachten und mit Differentialrechnung das Maximum bestimmen.
============
Je nachdem, wie weit ihr bei der Differentialrechnung seid [insbesondere bei Differentialrechnung mit mehreren Veränderlichen], könntest du auch die absoluten Extrema der Funktion...
... mit Hilfe der Differentialrechnung bestimmen. Da könnte man dann darauf kommen, dass das absolute Minimum bei der Stelle (-1/√(3), -1/√(3)) liegt und den Wert -3√(3)/8 hat, und dass das absolute Maximum bei der Stelle (1/√(3), 1/√(3)) liegt und den Wert 3√(3)/8 hat. Dementsprechend gilt dann für alle x, y ∈ ℝ die Abschätzung...
Du kannst OBDA annehmen, dass |x| >= |y| gilt
Dann gilt |x+y| <= 2|x|
Außerdem sind beide Faktoren im Nenner jeweils echt größer als 1, wenn du also einen entfernst, wird der Bruch größer.
Du kannst also den Zweiten Faktor nach oben abschätzen mit: 2|x|/(1+x^2) und das solltest du leicht nach oben abschätzen können (denn es ist beschränkt)
Kontrolle: (wenn ich mich nicht verrechnet habe) kannst du dann L=1 als Lipschitz konstante wählen.