Mathe Bildpunkte berechnen?
Die Punkte sind A1(2|1|4), A2(5|3|6) und A3(-1|2|5).
Wenn ich jetzt die Bildpunkte in der x1x3-Ebene ausrechnen will muss ich das dann so machen:
Vektor 2/1/4 + r x Vektor -1/8/3?
Und dann halt für x2=0:
1+8r=0
r= -1/8
Und dann einsetzen in die anfangs Gleichung?
Ich bin mir unsicher, ist das der richtige Weg?
Danke im Vorraus!
2 Antworten
1.Schritt: Gerdengleichung aufstellen
2.Schritt: Den Geradenparameter t berechnen
3.Schritt: Schnittpunkt mit der x1,x3 Ebene berechnen
Geradengleichung r=ro+t*a "Punkt-Richtungsgleichung" siehe Mathe-Formelbuch Kapitel "Vektorrechnung"
ro=S(-1/8/3) "Stützvekktor" /Stützpunkt)
A1=S+t*a ergibt mit t=1 A1-S
xA1- xS=2-(-1)=3 und yA1-yS=1-8=-7 und zA1-zS=4-3=1 also a=(3/-7/1)
GeradenGleichung ist r=(-1/8/3)+t*(3/-7/1)
In der Zeichnung sehen wir ein x-y-z-Koordinatensystem
x1=x und x2=y und x3=z
mit den Punkt yA´1=0 ergibt 0=yS+t*ya=8+t*-7 ergibt t=8/7=1,1426
Nun die Koordinaten von A´1 berechnen
xA´1=xS+1,1426*xa=-1+1,1428*3=2,4284
y´A1=0
zA´1=zS+t*za=3+1,1428*1=4,1428
Koordinaten von A´1 auf der Ebene also A´1=(2,4284/0/4,1428)
Die selbe Rechnung mit A´2 und A´3 durchführen.
Prüfe auf Rechen-u. Tippfehler
Hallo,
naja.
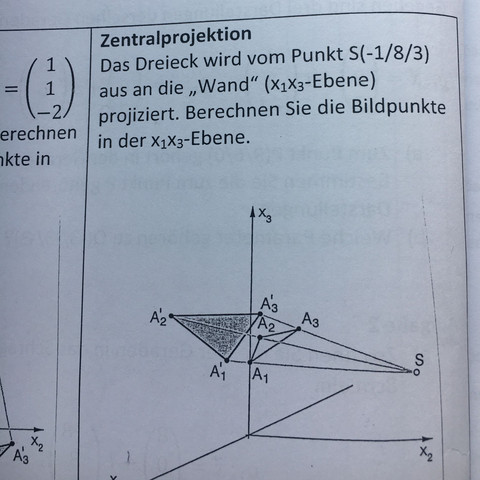
Du hast doch so eine schöne Skizze.
Was Du berechnen mußt, ist der Punkt, an dem die Strahlen, die von S zu A1, A2 und A3 führen, jeweils die x1x3-Ebene durchstoßen.
Du bildest also zunächst die Strahlen/ Geraden.
Am Beispiel von Punkt A1 mach ich Dir das mal vor.
Die Gerade, die von S über A1 Richtung x1x3-Ebene führt, ist
(-1/8/3)+s*(A1-S), also (-1/8/3)+s*(2-(-1)/1-8/4-3)=(-1/8/3)+s*(3/-7/1)
Die x1x3-Ebene hat die Gleichung v*(1/0/0)+w*(0/0/1)
Nun könntest Du ein Gleichungssystem mit drei Unbekannten aufstellen, um s, v und w zu berechnen. Das ist aber nicht nötig.
Egal, wo sich der Bildpunkt befindet: eins wissen wir ganz genau, er liegt in der x1x3-Ebene und damit ist seine x2-Koordinate auf jeden Fall gleich Null, denn sonst könnte er gar nicht in der Ebene liegen.
Es reicht also, zu berechnen, für welches s in der Geradengleichung die x2-Koordinate der Geraden gleich Null wird.
Wir stellen also einfach eine Gleichung aus den x2-Koordinaten der Geraden auf, indem wir sie auf Null setzen:
8-7s=0
7s=8
s=8/7
Nun wird s=8/7 in die Geradengleichung eingesetzt. So bekommen wir als Ergebnis A1'.
(-1/8/3)+(8/7)*(3/-7/1)=(17/7|0|29/7)=A1'
Mit den beiden anderen Punkten verfährst Du genauso.
Gerade aus S+s*(A2-S) bestimmen, x2-Koordinaten auf 0 setzen, s berechnen, s in Geradengleichung einsetzen, Punkt A2' berechnen und das Gleiche noch mal mit A3.
Herzliche Grüße,
Willy