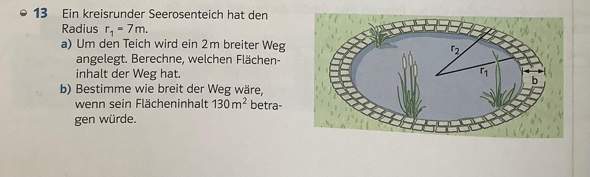
Wie kommt man bei solchen Matheaufgaben auf die lösung?
Hey,
ich schreibe demnächst eine Mathearbeit und muss mit solchen Aufgaben rechnen, aber ich verstehe sie überhaupt nicht und wollte fragen, ob mir jemand erklären kann, wie man auf die Lösung kommt. :(:
4 Antworten
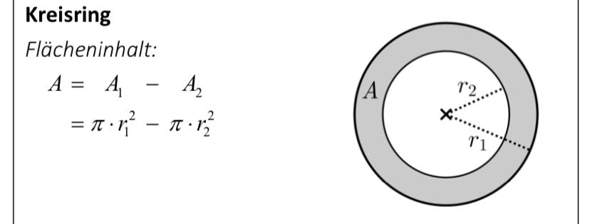
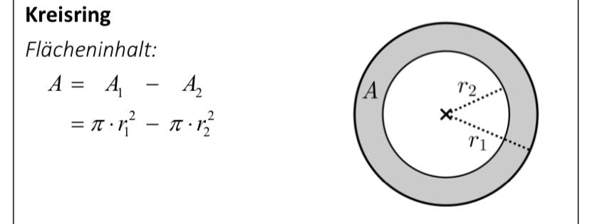
Großer minus kleiner Kreis ist die Fläche des Weges ( die Form nennt man "Kreisring"
.
Großer Kreis : Radius 7+2
Kleiner Kreis : Radius 7
.
Kreisfläche pi*r²
Daher
pi*(7+2)² - pi*7² = Kreisringfläche
.
b)
kniffelig ! die 7 Meter für den Teig bleiben , aber die 2 sind jetzt unbekannt !
Nehmen wir wieder die Formel von oben , aber bei der 2 kommt jetzt das x hin für unbekannt
pi*(7+x)² - pi*7² = 130
für weniger Rechenarbeit das pi ausklammern
pi * ( (7+x)² - 7² ) = 130
ausmulti
pi*( 49 + 14x + x² - 49 ) = 130
pi*(14x + x²) = 130
durch pi teilen und alles nach links
x² + 14x - 130/pi = 0
nun pq mit p = 14 und q = -130/pi
Für a) nimmst du am besten die Formeln für die Kreisringe. Du berechnest beide Kreise. Die Maße sind ja vorhanden. Anschließend nimmst du den kleinen Kreis und subtrahierst den mit dem großen Kreis. Dann hast du den Flächeninhalt für den äußeren Kreis.
b) da musst du mit der p-q-Formel arbeiten.
Formel für den Kreisring:
Formel für die p-q-Formel:
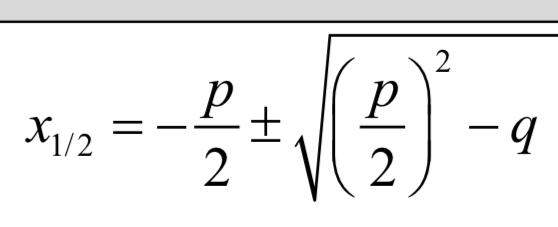
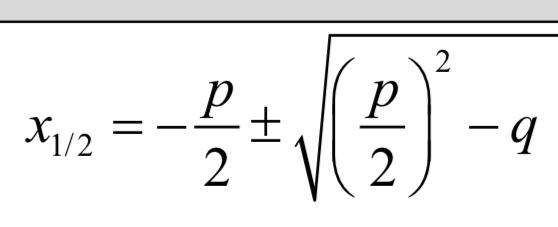
Hallo, also richtig sicher bin ich mir jetzt auch nicht. Allerdings kann ich sagen, dass du, wenn du den Flächeninhalt vom Teich(R1=7m) ausrechnest und dann von dem Flächeninhalt des Weges mit Teich(R2=9m) abziehst, du das Ergebnis hast. Soviel zu a).
Bei b) weiß ich auch nicht weiter.
Ich habe keine Ahnung ob das stimmt...
doch das stimmt .
bei b) ersetzt man die 2 aus a durch x und muss dann eine quadratische Glg lösen
Aufgabe b) aus dem Video ist gleich wie deine Aufgabe a), also sehr ähnlich.
https://www.youtube.com/watch?v=6rpLDDST8Hw
Such dir am besten erst mal alle Formeln zurecht, die brauchst du für den Kreisring.
Also ist pi*7 hoch zwei der Flächeninhalt ?