Kräfte berechnen Mechanik?
Tag! Man kann ja mit dem Kosinussatz ganz einfach die Resultierende aus 2 Kräften bilden.
Nur, dann habe ich ja die Kraft, aber wie weiß ich dann in welchem Winkel die Krft weggeht?
Kann man den auch berechnen?
2 Antworten
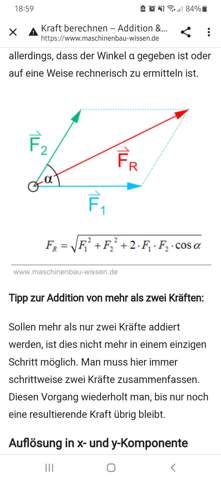
Den Winkel zwischen der resultierenden Kraft und einer der Ausgangskräfte kannst du ebenfalls mit dem Kosinussatz berechnen. Du hast hier ja ein Parallelogramm, das (vom Repräsentanten der Resultierenden) in zwei Dreiecke zerlegt wird; die Seiten dieses Dreiecks sind bekannt.
-----
Übrigens ist die Bemerkung im unteren Teil falsch: Das Addieren von beliebig vielen Vektoren (und Kräfte sind Vektoren) ist ohne Weiteres möglich - man zeichnet zu jedem Vektor (nach dem ersten) einfach einen Repräsentanten, der am Endpunkt des vorigen beginnt.
Falls dies als mehrere Schritte bezeichnet wird, besteht auch die Addition zweier Vektoren aus zwei Schritten: Zeichnen eines Repräsentanten des ersten Vektors; Zeichnen eines Repräsentanten des zweiten Vektors.
Das Parallelogramm ist nur ein Hilfsmittel. Zum Addieren reicht einer der beiden Wege - beim einen Weg wird zuerst F1 gezeichnet und F2 angehängt, beim anderen wird erst F2 gezeichnet und dann F1 angehängt. Hat eigentlich nur den Vorteil, dass man sofort sieht, wenn man ungenau gezeichnet hat.
Am einfachsten ist es, wenn man die Kräfte jeweils in eine x-Komponente und eine y-Komponente aufteilt. (Das ist immer möglich.) Dann kann man alle x-Komponenten und alle y-Komponenten getrennt addieren und erhält die x-Komponente und die y-Komponente der resultierenden Kraft.
Den Winkel erhält man dann als arctan(y/x) oder arctan(y/x) + 180°.
Stimmt🤔
Ja dann, danke vielmals!
Ich brauchs eigentlich nicht unbedingt, habe aber am Freitag die erste Schularbeit, müsste eigentlich nur das Graphische wissen, aber da wir ja sowieso den TR verwenden dürfen, tuts sicher keinen Schaden wenn ich auch rechnerisch kontrollieren kann odr!
Danke nochmals und ich wünsch dir noch eine gute Zeit!👍
Kann man den auch berechnen?
Ja - denn du hast ja dann ein Kräftedreieck in dem alle Winkel bekannt sind welche zu jedem Bezug errechnet werden können.
Danke erstmal!
Nur,
das wäre dann doch ein Kräfteparallelogram nicht?
Aber wie kann man den Winkel rein rechnerisch lösen, denn graphisch wird es ja ungenau?