Konstruiere eine Strecke der Länge Wurzel 12 cm?
Wie geht das nochmal? Ich soll nur die Strecke konstruieren, mehr nicht
4 Antworten
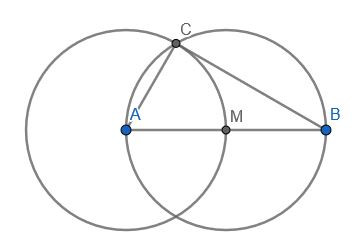
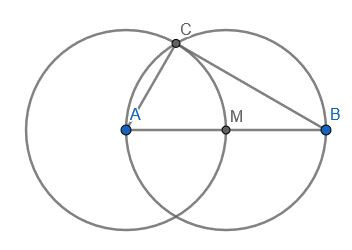
Hier also das Bild zur meiner Lösung. Es ist AB = 4, AC = 2, und BC ist dann automatisch eine Strecke mit der Länge wurzel(12)
da gibt's doch so eine Wurzelschnecke oder so
damit kann Wurzeln genau konstruieren
"Wurzelschnecke": das ist wohl die Konstruktion, bei der man nacheinander Strecken der Längen √(1), √(2), √(3), √(4), √(5), √(6), √(7), √(8), √(9), ... konstruiert. Das ist dann zwar "im Prinzip" exakt, aber in der Praxis wahrscheinlich ziemlich ungenau wegen der großen Zahl der Konstruktionsschritte. Wenn dann noch Bleistift und Zirkelstift nicht richtig gespitzt sind und man wenigstens einmal ein wenig verrutscht, ist das Ergebnis kaum noch brauchbar !
Was willst du benutzen? Pythagoras, Kathetensatz, Höhensatz? Es geht mit allen dreien.
Wie meinst du das genau mit dem Thaleskreis und dem Kreis mit r=2cm?
Du musst 12 als Summe oder Differenz von zwei Quadratzahlen darstellen, hier fällt mir spontan 12 = 16 - 4 ein, also
12 = 4^2 - 2^2.
Du zeichnest also eine Strecke von 4cm, darüber einen Thaleskreis (wegen des rechten Winkels), dann einen Kreis mit r = 2cm (die erste Kathete), wo die beiden Kreise sich treffen, da ist der Punkt C (rechte Winkel) des Dreiecks. Die andere Strecke hat dann die Länge wurzel(12).
Denke mal an ein Quadrat und die Länge der Diagonalen. Kommt Dir da eine Idee?
pythagoras