Könnt ihr mir bitte sagen, ob meine Antwort richtig ist (Mathe Oberstufe)?

2cos²(x)=sin(x) //nur im Intervall von 0≤x≤2pi

2(1-sin²(x))-sin(x)=0

2-2sin²(x)-sin(x)=0

2-2z²-z=0

dann habe ich die ABC Formel angewendet und kam auf:

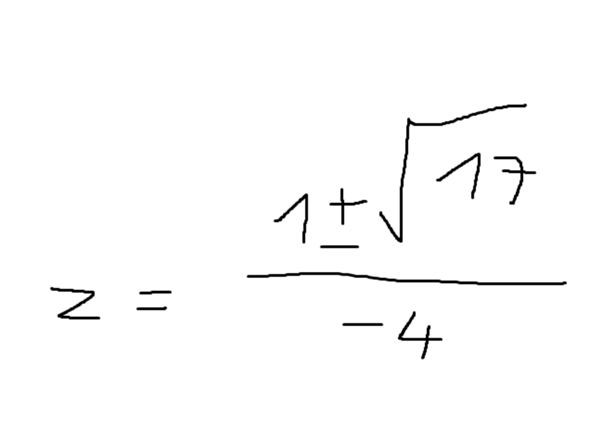
Bild zum Beitrag

Nun, kann ich für u = sin(x) einsetzen und mithilfe Arkussinus x berechnen.

Meine Lösung war, dass im Intervall von 0≤x≤2pi es keine Reale Lösung gibt, was bedeutet, dass es keine reellen Zahlen im Intervall für x gibt. Stimmt das? Würde mir helfen, es zu wissen. Danke für die Zeit und Aufmerksamkeit.

3 Antworten

Maxi170703

Von gutefrage auf Grund seines Wissens auf einem Fachgebiet ausgezeichneter Nutzer

Gleichungen, Mathematik

11.10.2023, 20:02

Bis zur Rücksubstitution stimmt das. Der Sinus nimmt aber durchaus den Wert -1/4 + sqrt(17)/4 im Intervall 0 <= x <= 2pi an, sodass es auch Lösungen für x gibt. Genauer gesagt 2 Lösungen etwas links und rechts von Pi/2.

Woher ich das weiß:Studium / Ausbildung – Maschinenbaustudent, RWTH Aachen

Halbrecht

Von gutefrage auf Grund seines Wissens auf einem Fachgebiet ausgezeichneter Nutzer

Gleichungen, Sinus, Mathematik

11.10.2023, 20:01

so sieht es aus :

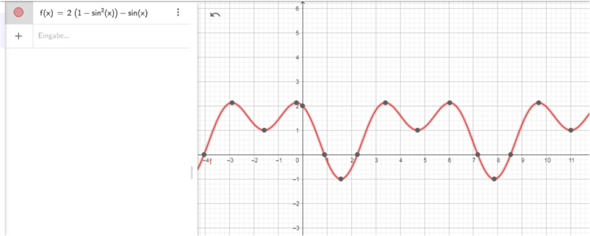
Bild zum Beitrag

es sollten also ZWEI Lösungen zu finden sein

-1/4 + wur(17)/4 = -1/4 + ca 1 = ca -0.750 . geht also

Maxi170703

11.10.2023, 20:33

= ca +0,75 ;)

Tannibi

Nutzer, der sehr aktiv auf gutefrage ist

im Thema Gleichungen

11.10.2023, 20:03

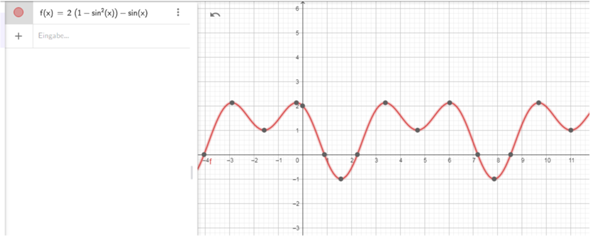
Da hast du was falsch gerechnet. Als brauchbarer Wert kommt z = 0.781 raus.

Ähnliche Beiträge

Wie löse ich die trigonometrische Gleichung sin(2x)=0,5 korrekt?

Ich bin mit dem Weg über der Substitution vorgegangen, aber irgendwie ist meine Lösung falsch.

(Intervall ist 0;2pi)

sin(2x) = 0,5 I Substitution u = 2x

sin(u) = 0,5 I WTR

u = pi/6

Resubstitution: u = 2x

pi/6 = 2x I *0,5

pi/12 = x

Periodenlänge: 2pi/b = 2pi/2 = pi

x1= pi/12

x2 = pi/12 + pi = 13pi/12

Ich weiß nicht, wie ich es sonst lösen sollte. LG

...zum Beitrag

Wie vereinfacht man diese Gleichung?

Ich habe die Gleichung bei Photomath eingegeben, verstehe aber trotzdem nicht wie man auf die Lösung kommt.

Ich komme leider nur bis cos(x)^2+ 2cos(x)sin(x)- sin(x)^2

Könnt ihr mit bitte helfen wie ich weiterkomme? Vielen Dank schon mal!

...zum Beitrag

Intervall angeben in dem sin(x) umkehrbar ist?

Halloo, ich bin mir bewusst, dass sin(x) immer umkehrbar auf einem gewissen Intervall ist da es entweder fällt oder steigt, aner wie kann man das mathematisch korrekt angeben?

in der Lösung bei schwafeln die etwas von (keZ) . Mein lHerer will, dass wir unsere Lösungen immer allgemein angeben und nicht anhand von Beispielen, kann mir da einer bitte helfen?

Vielen Dank

...zum Beitrag

Nullstellen Sinus?

Hallo zusammen,

ich sitze gerade an einer Klausuraufgabe zu dem "Mathematischen Grundlagen der Ingenieurwissenschaften", nämlich:

Gegeben ist die Funktion

f(x)=2 * sin(x - pi) + 2

Die Aufgabe ist, dass ich die Nullstellen berechnen soll und die Funktion zeichnen soll.

Die Nullstellen, die ich ausgerechnet habe, lauten x = k * pi + pi (mit k in Z)

Laut Lösung meines Professors lauten die Nullstellen aber x = pi/2 + 2pi * k, aber warum?

Die Nullstellen wiederholen sich doch alle Pi und nicht alle 2Pi, auch wenn Sinus 2Pi-periodisch ist.

Mein Ansatz war:

x - pi = k * pi

x = pi + k * pi

Kann mir irgendjemand helfen?

Danke!

...zum Beitrag

Reelle Lösungen von "(sin(2x) + 1)=0"?

Meiner Meinung nach müsste die Lösung "x=3π/4 + kπ (k ∈ Z)" sein.

Die Lösung sagt aber "x = − π /4 + kπ (k ∈ Z)" sei Richtig, liege ich falsch oder ist die Lösung einfach nur fehlerhaft?

...zum Beitrag

Trigonometrie Gleichungen Lösen wie?

also...wir haben ein neues Thema im online Unterricht bekommen und zwar: Trigonometrie geichungen....und ich verstehe es glaube ich nicht so ganz.

Bestimme jeweils alle Lösungen der Gleichung im Intervall (0; 2pi)

(1) sin(x) = 0,4

(2) sin(x) = -0,2

(3) sin(x) = 1

(4) sin(x)= 0,866025404

Wie mache ich das jetzt? Meine Idee war:

(1) sin(x) = 0,4

dann sin hoch minus 1(0,4) = 0,411516

ABER JETZT KOMME ICH NICHT WEITER....muss ich jetzt einfach nur noch:

sin(x)=sin(pi - 0,411516)= 0,3995???

ANGEBLICH IST DAS LAUT LEHRERIN FALSCH....und ich verstehe nicht wie das anders gehen soll.

...zum Beitrag

Trigonometrische Gleichungen im Intervall lösen?

Die Aufgabe lautet folgendermaßen: Bestimmen Sie die Lösungen der Gleichungen im Intervall [0; 4π]. Geben Sie die Lösung sowohl in Bogen- als auch in Gradmaß an.

a)sin(α)=0,4

b)cos(α)=0,5

c)tan(α)=0,8

Meine Frage ist nun, was bestimme ich das? Trigonometrie, Intervall, Bogenmaß, Gradmaß...was soll das alles bedeuten? Ich habe absolut keinen Plan was ich machen soll, wäre ganz nett wenn mir jemand helfen könnte :D Danke im Voraus

...zum Beitrag

Funktionsuntersuchung Sinusfunktion 2*sin(x) + sin(2x)?

Ich habe folgende Sinusfunktion gegeben:

f(x) = 2*sin(x) + sin(2x)

Ableitung:

f'(x) = 2*cos(x) + 2*cos(2x)

Die Nullstellen waren kein Problem, aber die Extrema sind irgendwie verzwackt:

0 = 2cos(x) + 2*cos(2x)

0 = cos(x) + cos(2x)

Aus cos(2x) kann man noch folgendes machen:

0 = cos(x) + ( cos²(x) - sin²(x) )

Oder auch:

0 = cos(x) + ( 1 - 2sin²(x) ) oder 0 = cos(x) + ( 2cos²(x)-1 )

Ab da weiß ich nicht weiter.

Man könnte auch die Ausgangssituation der notwendigen Bedingung nehmen:

cos(x) = -cos(2x)

Aber das hilft auch nicht wirklich weiter oder?

Wie finde ich die exakten Extremstellen raus? Ich hoffe mir kann jemand helfen!

Vielen Dank im Voraus

...zum Beitrag

Frage zu Mathematik Funktionen Additionstheoreme?

Hallo! Habe ein Problem mit folgender Aufgabe:

Bestimmen Sie die Lösungsmenge L der Gleichung:

sqrt(3) * sin(x/2) + 3 * cos(x/2) = 0 im Intervall [0 , 2pi)

die Lösung des Beispiels ist als "4pi/3" angegeben.

mir selbst kommt leider nur genau die hälfte raus.

----------------------------------

Meine Rechnung:

sqrt(3) * sin(x/2) + 3 * cos(x/2) = 0 .................../ - 3 * cos(x/2)

sqrt(3) * sin(x/2) = -3 * cos(x/2) ......................../ ^2

3 * sin^2(x/2) = 9 * cos^2(x/2) .........................../ : 3

sin^2(x/2) = 3 * cos^2(x/2) ................................./ sin^2(x) = 1 - cos^2(x)

1 - cos^2(x/2) = 3 * cos^2(x/2) .........................../ + cos^2(x/2)

1 = 4 * cos^2(x/2) ................................................/ : 4

1/4 = cos^2(x/2) ................................................../ sqrt()

1/2 = cos(x/2) ...................................................../ arccos()

arccos(1/2) = x/2 ................................................/ * 2

x = 2 * arccos(1/2)

2 * arccos(1/2) = 2pi/3 ; richtige Lösung is aber 4pi/3

----------------------------------

Ich habe leider keine Ahnung wo ich falsch abgebogen bin, daher wäre ich sehr dankbar, wenn mir jemand helfen würde.

Vielen Dank im Voraus!

LG Fisch

...zum Beitrag

Sinus- und Cosinusgleichung?

Wie kann ich die Gleichung sin(x) + cos(x) = 1/(Wurzel 2) lösen, so dass ich alle reellen Lösungen angeben kann?

Hab leider noch keine Idee ...

...zum Beitrag

Funktion in Sinusfunktion umstellen?

Hallo, hier ist eine Aufgabe bei der ich nicht weiter komme.

Man muss den Funktionsterm f(x) = 2sin(2x+pi) in die Form f(x)= a×sin(b×(x-c)) bringen.

Die lösung gibt vor dass es f(x) = sin(2×(x+pi/2)) ist. Kann es sein dass die Lösung vielleicht falsch ist? Ist bei unserem Buch öfters so.

Wäre nett wenn ihr mir auch erklärt, wie ihr vorgegangen seid.

...zum Beitrag

Sinus- und Kosinusfunktion - Lösungen im Intervall angeben?

Hallo Experte! Ich brauche deine Hilfe 💪

Hier ist ja in der Klammer von Sinus vor dem x noch „pi/3“. Deshalb muss ich die Periode „p = 2pi / k“ ausrechnen. Hierbei verstehe ich nicht das Ergebnis. Was kann ich mit dem Ergebnis anfangen (unter dem Aufgabenbild ist meine Rechnung)?

“Geben Sie alle exakten Lösungen im Intervall [0; 2pi] an.“

—> Berechnung der Periode:

p = 2pi / k

p = 2pi / (pi/3)

p = 6

Bei anderen Aufgaben kommt immer „p = Zahl pi“ raus. Also immer ein pi dahinter. Und eine Zeichnung von Sinus zum Beispiel geht immer bis 2pi bis der ganze „Kreis“ abgebildet ist.

(Beispiel andere Aufgabe, wo ich es verstehe:

Intervall [0; 2pi]

cos(x/2) = 0,5

—> Berechnung der Periode:

p = 2pi / k

p = 2pi / (1/2)

p = 4pi

)

Was fange ich also mit dem Ergebnis der Periode bei meiner Aufgabe von „p = 6“ an?

Meine Rechnung (falsch, x1 müsste 3,5 sein):

...zum Beitrag

Berechne die Fläche von f(x)=sinx im Intervall 0 und 2pi?

Brauch etwas hilfe bei dieser integral Aufgabe.

Es ist keine bewertete Hausaufgabe o.ä. Ich bin lediglich am üben und komme bei dieser Aufgabe auf keine gescheite Lösung

Danke

...zum Beitrag

In welchem Intervall ist f(x) = sin (x) bijektiv?

Durch ausprobieren mitm Taschenrechner komme ich auf [-0,5 Pi | 0,5 Pi]. Gibts eine mathematische Lösung, bzw. eine die ohne Ausprobieren mit dem Taschenrechner auskommt?

...zum Beitrag

Was möchtest Du wissen?

Deine Frage stellen