Goniometrie?
Kann mir bitte jemand das Thema Goniometrie anschaulich erklären, dass ich es nachher verstehe:). Vielen Dank
3 Antworten
KI hilft auch
Goniometrie, auch bekannt als Trigonometrie, befasst sich mit den Beziehungen zwischen den Winkeln und Seiten von Dreiecken. Hier sind die Grundlagen:
- Winkel und Seiten: In einem rechtwinkligen Dreieck gibt es drei Seiten: die Hypotenuse (die längste Seite gegenüber dem rechten Winkel), die Ankathete (die Seite neben dem betrachteten Winkel) und die Gegenkathete (die Seite gegenüber dem betrachteten Winkel).
- Trigonometrische Funktionen: Diese Funktionen helfen, die Beziehungen zwischen den Winkeln und den Seiten zu verstehen:
- Sinus (sin): Verhältnis von Gegenkathete zur Hypotenuse.
- Kosinus (cos): Verhältnis von Ankathete zur Hypotenuse.
- Tangens (tan): Verhältnis von Gegenkathete zur Ankathete.
- Anwendung: Mit diesen Funktionen kannst du Winkel berechnen, wenn du die Seitenlängen kennst, oder umgekehrt.
Ein Beispiel: Wenn du in einem Dreieck die Länge der Gegenkathete und der Hypotenuse kennst, kannst du den Sinus des Winkels berechnen und so den Winkel selbst bestimmen.
und immer dran denken : der KI darf man nur vertrauen , wenn man das Thema selbst gut kennt.
Danke für ihre Hilfe aber ich habe mühe beim auflösen von Gleichungen und finden von Lösungen. Ich weiss aber um was es im Thema geht und auch was berechnen aber ich verstehe nicht wie.
Um goniometrische (trigonometrische) Gleichungen lösen zu können - ich denke, darum geht es Dir - sind Kenntnisse über den Verlauf trigonometrischer Funktionen erforderlich, insbesondere hinsichtlich Symmetrie und Periodizität, da ohne Vorgabe eines Intervalls unendlich viele Lösungen möglich sind.
Kenntnisse über Komplementbeziehungen (z.B. sin(x) = cos(90° - x)), über Reduktionsformeln (z.B. sin(360° - x) = -sin(x)), über Additionstheoreme (z.B. sin(x + y) = sin(x) * cos(y) + cos(x) * sin(y)), über Funktionen doppelter und halber Winkel (z.B. sin(2x) = 2 * sin(x) * cos(x)), ... sind hilfreich und oftmals auch notwendig.
Bei youtube gibt es zahlreiche Videos zum Thema. Beginne mit einfachen Aufgaben. Übung macht den Meister.
beispiel : diese Glg

um die zu lösen , nutzt man die Beziehung tan(x) = sin(x) / cos(x)
Zeile 2 entsteht durch das Teilen durch cos(x)
sin(x)/cos(x) + k * cos(x)/cos(x) = 0/cos(x)
tan(x) + k*1 = 0
tan(x) = -k
arctan(x) muss man kennen ( das ist auf dem TR tan^-1 ) , und die Periode von tan(x) ( die ist pi )
mehr davon hier ( mit einigen Lösungsschritten )
Die nutzen vieles hiervon

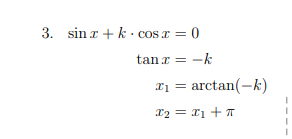

Die sind echt gut, Danke! Aber wie komm ich dann auf die Lösungen? Wenn ich die Aufgaben vereinfacht habe muss ich sie dann nur noch im Taschenrechner eingeben und dann stimmt es? Meistens hat es ja immer zwei Lösungen die ich finden muss in einer Periode.
in den TR ? meinst du arctan ? das geht nur mit dem TR
Aber auch die Lösung arctan(k) ist möglich ,wenn keine Zahl für k gegeben ist
mehr als zwei Lösungen sind gut möglich , wenn im Intervall 0...2pi gesucht werden soll , die Periode aber z.b pi/4 ist
danke aber das ist ja Trigometrie und nicht Goniometrie… Grundlagen für die Goniometrie die man sicher beherrschen muss.