Frage zum Schiefen Wurf (Mechanik)?
Wie mach ich bei dieser Aufgabe weiter?
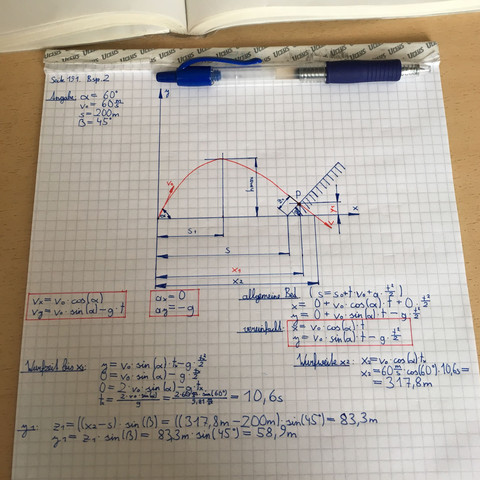
Ist das bis jetzt richtig?
Aufgabe 2
Danke

4 Antworten
Es geht hier nur um den Schnittpunkt 2 .er Funktionen.
1. Die Geradengleichung der Wand y= m *x +b= 1 *x -200
2. Die "Wurfparabel " y=f(x)= - 1/2 *g * x^2/Vo^2 * cos^2(a) +tan(a) *x
hab ikke aus´n Physik-Formelbuch abgeschrieben,was man privat in jden Buchladen bekommt.
3. Gleichsetzen der beiden Funktionen
Zuerst rechnen wir die bekannten Zahlen aus,das wird dann übersichtlicher
g=9,81 m/s^2 und Vo= 60 m/s und Winkel Alpha (a)= 60°
also - 9,81/(2 * 60^2 * cos^2(60°)= - 5,45 *10^(- 3)
tan(60°)=1,732
y=f(x)= - 5,45 *10^(-3) * x^2 + 1,732 * x = 1 * x - 200
0= - 5,45 *10^(-3) * x^2 +1,732 * x - 1*x + 200
Parabel ist somit 0= - 5,45*10^(-3) * x^2 +0,732 * x + 200
Lösung mit meinen GTR (Casio) x1= - 135,8 m x2= 270,15 m
Die Kugel trifft die Wand bei x= 270,15 m und y=1 *270,15-200=70,15 m
Y= - 5,45 *10^8-3) * x^2 + 1,732 * x
y= -5,45 *10^(-3) * 270,15^2 + 1,732 *270,15=70,15 m
Herleitung der "Wurfparabel"
1. in x-Richtung x= Vo *cos(a) * t ergibt t= x/(vo *cos(a))
2. in y-Richtung y=f(t)= - 1/2 *g * t^2+ Vo * sin(a) * t
1. in 2. y= - 1/2 *g * x^2/(Vo^2 * cos^2(a)) + Vo * sin(a) * x/(Vo * cos(a))
mit tan(a)= sin(a)/cos(a) ergibt sich die "Wurfparabel"
y=f(x)= - 1/2 * g * x^2(Vo^2 * cos^2(a))+ tan(a) *x
Herleitung der Geraden für die Wand y=f(x)= m *x +b
mit tan(45°)=m=1 ergibt sich y=0= 1 * 200 + b also b= - 200
Geradengleichung für die Wand somit y=f(x)= 1 *x - 200 m
prüfe auf Rechen-u.Tippfehler !
Hallo . . Du bist die Aufgabe sehr sauber und systematisch angegangen! Sonderlob!
y1 und y1 sind sicher gesucht. Deinen Weg habe ich nicht im Detail nachvollzogen.
Ich würde die Aufgabe so angehen:
1. Wurfparabel / Bahngleichung ansetzen
2. Die Gerade der Schräge: y_s = (x-s) für x >/=s verwenden
und den Schnittpunkt der beiden bestimmen.
Falls dein Lösungsweg zum Einschlagpunkt führt oder du meine Anregung aufgreifst..... wenn du x1 hast >>>> über die horizontalkomponente der Abwurfgeschwindigkeit die Zeit bestimmen (Horizontakkomponente ändert sich nicht)
Das wird dir bestimmt weiterhelfen simple und leicht zu verstehen:
http://www.leifiphysik.de/mechanik/waagerechter-und-schraeger-wurf/schraeger-wurf
Da steht keine Aufgabe ? lediglich die Beschreibung eines hypothetischen Kugelwurfs.
Danke für das Lob und die Antwort.
Die Wurfzeit ist gesucht. Ich weiß leider nicht weiter.
Lg