Flächeninhalt Dreieck?
kann mir jemand please das einfach beantworten, ich werdes dann einfach verstehen.
die Aufgabe lautet: b=50, a=30, gemma= 120 grad
also das problem ist halt, dass ich noch nicht eine Aufgabe mit sin,cos,tan über 90 grad gerechnet hab, wäre megaaaa lieb wenn ihr es rechnet und jeden rechenschritt aufschreibt.
ich wollte es vielleicht mit Sinus satz machen, aber wir haben ja kein c und kein Beta/alpha ( wir haben cos satz noch nicht gemacht)
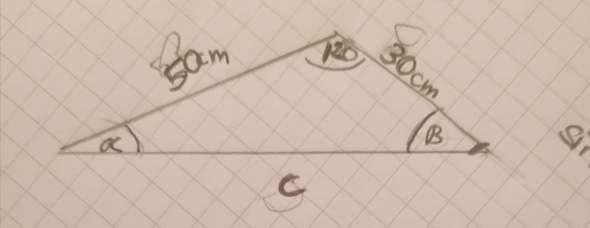
Hier
ne skizze oder ein bild?
Ich habe jetzt eine hochgeladen
2 Antworten
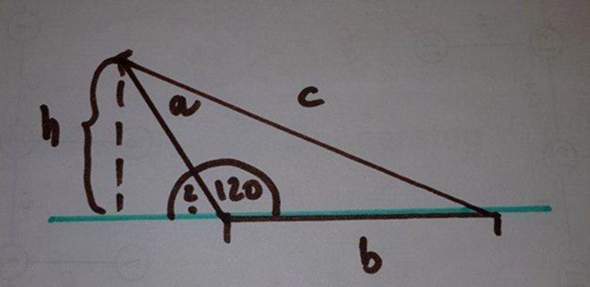
Zeichne es dir auf, mit b oder a als Grundseite. Dann siehst du, dass du mit dem Gegenwinkel 60° rechnen kannst, und dann ganz normal mit dem Sinussatz die Höhe berechnest. Die Höhe liegt in diesem Fall ja außerhalb des Dreiecks.
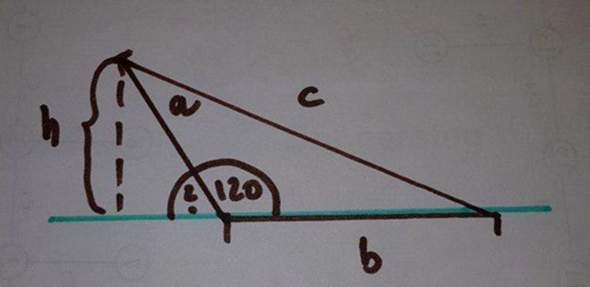
Ich hab mal ein Bild eingefügt. Wie groß ist der Winkel beim Fragezeichen? Du willst du Höhe h ausrechen. Du kennst a und den Winkel beim Fragezeichen... Also?
Deine Zeichnung hat c als Grundseite. Damit machst du es dir unnötig schwer. c kennst du ja nicht. Und c brauchst du auch gar nicht zu berechnen, du willst ja den Flächeninhalt, dafür reicht a oder b und die entsprechende Höhe dazu.
Hi,
siehe Bild mit Rechnung:
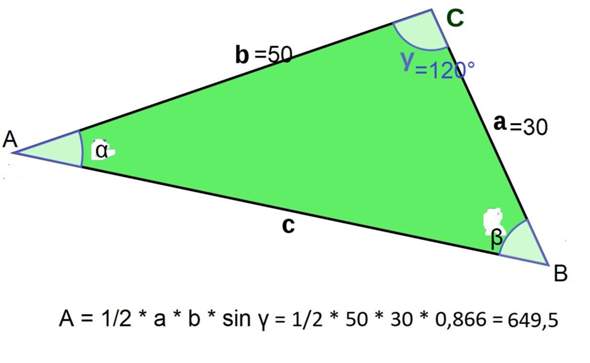
Es gibt diese Formel zur Berechnung der Fläche, man braucht weiter gar nichts!
LG,
Heni
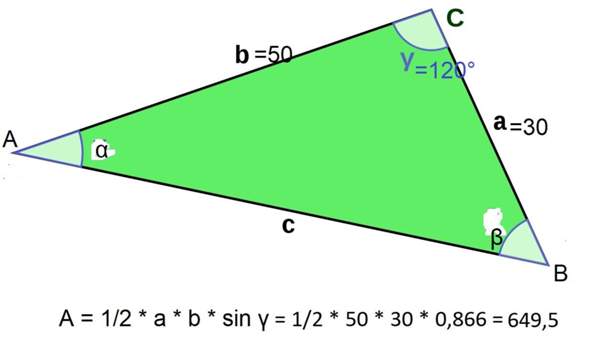
Und.... warum gilt diese Formel? Soll man jetzt für jeden Fall (SWS, WSW, etc.) die Formel auswendig lernen? Wann genau gilt die?
Das habe ich jetzt von Dir nicht erwartet dass Du diese Formel nicht kennst!
Hier die Formel und ein Video zur Herleitung:
https://de.serlo.org/mathe/83525/fl%C3%A4cheninhalt-allgemeines-dreieck-mit-dem-sinus
Die Formel ist inzwischen so üblich, dass man sie beherrscht!
LG,
Heni
Ich halte sehr wenig davon, Formeln auswendig zu lernen, die sich mit einem Blick auf den Sachverhalt sofort rekonstruieren lassen. Die Seiten könnten auch ganz andere Namen haben, der Sachverhalt bliebe der gleiche, die Formel stimmt dann nicht mehr. Außerdem gibt es - wie gesagt - viele andere Fälle, die von dieser Formel nicht abgedeckt werden. Dann lieber das Problem verstehen.
Ich ebenfalls, aber ich wette fast dass diese Formel sogar im Buch des FS ist, sobald er solche Aufgaben bekommt.
Außerdem aus Deiner Skizze kann man sie sehr schnell herleiten, denn
hb = a * sin 60° (sin 120° = 180° - sin 60°), also hb = a * sin γ
und A = (1/2) * a * b * sin γ
Eben, darum habe ich ja auch die Skizze gemacht. Natürlich kann man das daraus herleiten, ja, darum geht es doch... Man hat einen Sachverhalt, zeichnet den auf, weiß, was der Sinus ist, fertig. Außerhalb der Schule heißen leider die Seiten meistens nicht a, b und c, die Winkel nicht alpha, beta und gamma - und schon hilft einem eine bloße Formel nix.
Ja, aber.... Du weißt es doch auch, dass die Schüler heute ohne Formel nicht weikterkommen!
Hast Doch sicher schon oft Fragen gelesen: "...ich brauche nicht die Lösung, nur die Formel zur Berechnung...."
Weil wenn wir zb. b als grundseite nehmen, dann wird gemma immer noch 120 Grad sein. Aber die Winkelsumme wäre dann doch zu groß??