Extremalprobleme mit Graphen, Nebenbedingungen?
Wie komme ich bei dieser Aufgabe auf die Nebenbedingung a=2x?
Ist mir total schleierhaft
Danke
3 Antworten
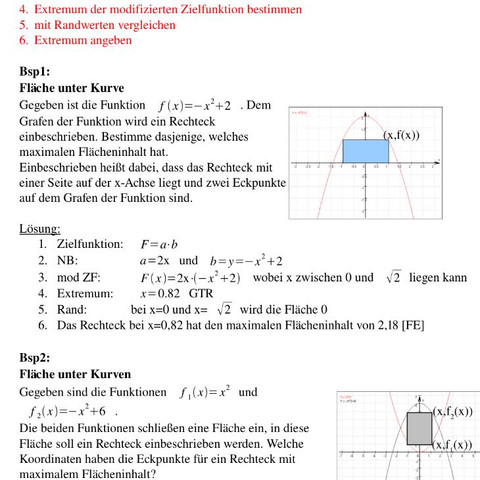
Das ist wegen der Symmetrie der Parabel so. x ist der Wert der halben Rechtecklänge wo der obere Eckpunkt des Rechtecks den Graphen der Funktion berührt, weil wegen der Symmetrie die rechte Seite rechts von der y - Achse genauso aussieht wie die linke Seite links von der y-Achse, deshalb 2 * x
Flächeninhalt des Rechtecks ist A=a *b =y * x oder A=f(x) * x
eingesetzt A=(- x^2 +2) * x=- x^3 +2 *x der Rest ist nur eine Kurvendiskussion ,hier nur die Berechnung eines Extremwertes.
abgeleitet A´= - 3 *x^2 +2 mit 0=- 3 *x^2 + 2 ergibt x= Wurzel (2/3) = +/- 0,816
A=0,8165 * 2 *- (0,8165^2 + 2) = 2,176 FE (Flächeneinheiten.
Hinweis : Die Formel A=f(x) *x funktioniert nur ,wenn der Graph nach unten offen ist und symetrisch zur y-Achse liegt !!
Bei der Funktion y= 2 * (x -2)^2 - 1 zum Beispiel,funktioniert das nicht !!
die Länge vom Rechteck ist 2x
ein x nach rechts und eins nach links wegen Symmetrie der Parabel.
Danke!!!!