E-Funktion 2 mal ableiten (Mathe)?
Wie geht es hier weiter? Ist das überhaupt richtig gelöst?
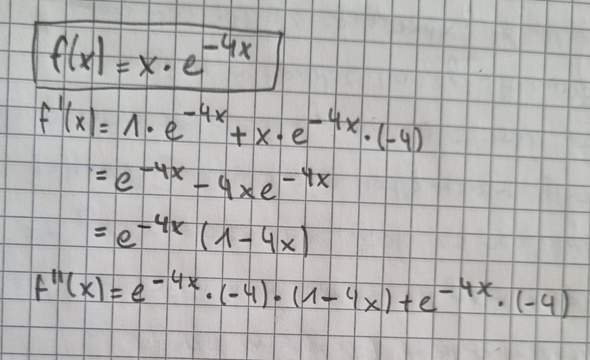
3 Antworten
Das ist richtig gelöst, jetzt nur noch wie bei der ersten Ableitung auch vernünftig zusammen fassen, dazu das e^(-4x) wieder ausklammern und die verbleibenden Terme ausrechnen.
Nein, jetzt mußt du üben mit negativen Zahlen korrekt zu rechnen.
Nun noch in der richtigen Reihenfolge und mit korrekten Klammern, dann passt es.
Das ist nicht korrekt sortiert und macht es damit unübersichtlich. Eine ganzrationale Funktion sortiert man immer von der höchsten zur niedrigsten Potenz, nciht umgekehrt.
Also muss es so aussehen: (-8+16x) e ^(-4x)
nein, was an "höchste Potenz zuerst" ist missverständlich? f''(x) = (16x - 8)e^(-4x)
Nebenbei enthält eine Funktionsgleichung immer ein "=".
Dir mag das alles als Erbsenzählerei erscheinen. Glaube mir bitte wenn ich dir sage dass es wirklich wichtig ist gewisse Formalismen einzuhalten. Gleichungen können deutlich komplizierter werden als dass was du da vorliegen hast. Wenn du da keine klaren Regeln einhälst verlierst du den Überblick und alles ist zu spät.
Ich glaube Ihnen das natürlich! Daher versuche ich auch ganz viel zu üben. Aber wie würde es denn richtig lauten?
Das ist richtig so und wenn du nur zweimal ableiten sollst, bist du auch schon fertig. Generell empfiehlt es sich bei der e-Funktion in Kombination mit der Produktregel aber immer, die e-Funktion nach dem Ableiten auszuklammern, falls man danach noch was mit der Ableitung machen muss.
sicher, dass ich fertig bin? Denn in der Lösung steht f´´(x)=4e^(-4x)*(4x-2)
Ja, das ist eben die Lösung mit Ausklammern. Das hast du ja bei der ersten Ableitung auch schon gemacht, um dann bequemer nochmal abzuleiten. Du kannst ja die e-Funktion wieder ausklammern und schauen, ob du auf das Ergebnis kommst.
Man könnte die 2.Ableitung etwas vereinfachen
mit (-4+16x)×e^-4x
Die 3. Ableitung wäre dann:
(32-64x)×e^-4x
Ansonsten stimmt dein Weg.
Vielen Dank! Ich habe es nun zusammengefasst: e^ (-4x) (-4+16x-4) ist dies richtig?