Bremsweg Berechnen?
Ich habe diese Frage zum Bremsweg eines Autos, ich kann die leider nicht lösen, aber vielleicht hier jemand? Ein Foto ist im Anhang. Ich möchte hier noch hinzufügen, dass der Bremsweg mit erhöhter Geschwindigkeit annähernd exponentiell ist (doppelte Geschwindigkeit=vierfacher Bremsweg)

3 Antworten
Wir haben 2 Gleichungen gegeben: Die erste beschreibt den Abfall der Geschwindigkeit (auf 0) und die zweite den zurückgelegten Weg:
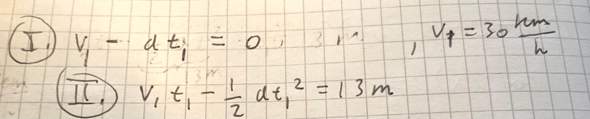
Da wir auch 2 Unbekannte haben (Verzögerung a und die Bremszeit t1), können wir sie durch die 2 Gleichungen ermitteln:
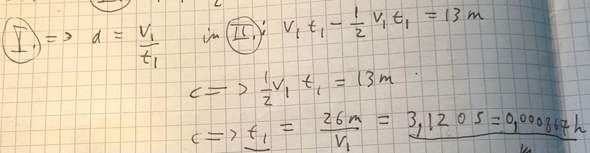
Gesucht ist nun die Geschwindigkeit Δv, die man nach der gleichen Verzögerung a und der gleichen Bremszeit t1 erhält, wenn man v2 = 50 km/h als Anfangsgeschwindigkeit hat.
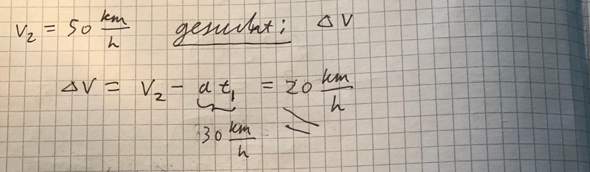
Das Ergebnis ist also 20 km/h.
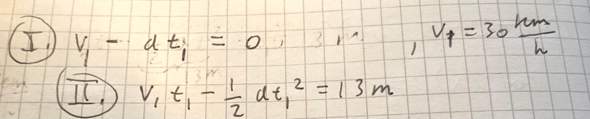
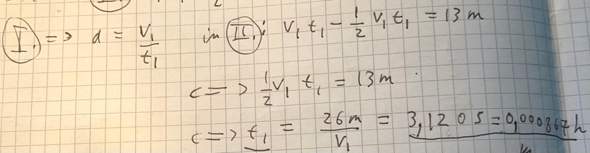
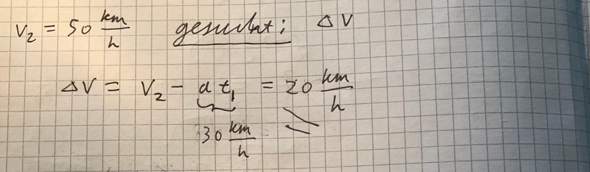
Es ist nicht die Geschwindigkeit gesucht, die nach der Bremszeit t1 noch vorliegt, sondern die, die nach dem Bremsweg s=13m vorliegt.
Die Fragestellung spricht außerdem von Anhalteweg, der sich aus Reaktionsweg und Bremsweg zusammensetzt. Die Rechnung betrachtet nur den Bremsweg (bei gleichmäßig verzögerter Bewegung).
Hallo,
der Anhalteweg setzt sich aus dem Weg, der in der Reaktionszeit ungebremst zurückgelegt wird, und dem eigentlichen Bremsweg zusammen.
Bei 50 km/h legt man in der Sekunde etwa 14 m zurück.
Das ist länger als der Anhalteweg bei 30 km/h.
Wenn der langsamere Wagen bereits steht, hat der schnellere noch nicht einmal damit angefangen, seine Geschwindigkeit zu verringern, weil er diese 13 m innerhalb der sogenannten 'Schrecksekunde' zurücklegt. Er hat also immer noch 50 km/h auf dem Tacho.
Herzliche Grüße,
Willy
Es geht um den Anhalteweg. Dieser setzt sich aus Reaktionsweg und Bremsweg zusammen.
Nach der Faustformel, die man in der Fahrschule lernt, beträgt alleine der Reaktionsweg bei 50km/h 15m. Nach 13m hat man also noch nicht einmal auf die Bremse getreten und fäht somit noch mit 50km/h.
Wieso, hat der langsamere Fahrer denn keine Schrecksekunde?