Boolesche Algebra umformen?
Moin,
eventuell kann mir einer bei einer Umformung boolescher Algebra für einen mathematischen Beweis helfen. Es schreit in mir entweder nach Distributivgesetz oder DeMorgan, mir fehlt aber noch der konkrete Ansatz.
Ich muss den folgenden booleschen Ausdruck:
mit Zwischenschritten in diesen umformen:
Die Äquivalenz beider Ausdrücke habe ich mittels Wahrheitstabelle geprüft, es handelt sich einfach klassisch um a XOR b. Mir fehlt aber wie gesagt der Ansatz, um von Ausdruck 1 auf 2 zu gelangen.
3 Antworten
Muss die Umformung in diese Richtung sein? Andersrum ist sie einfach, da klappt's mit De Morgan. Allerdings basiert die Umformung darauf, dass zwei nicht erfüllbare Ausdrücke rausfallen, deshalb tu ich mir sehr schwer, das andersrum zu machen. Dann müssen nämlich zwei nicht erfüllbare dazu kommen.
(Ergänzt)
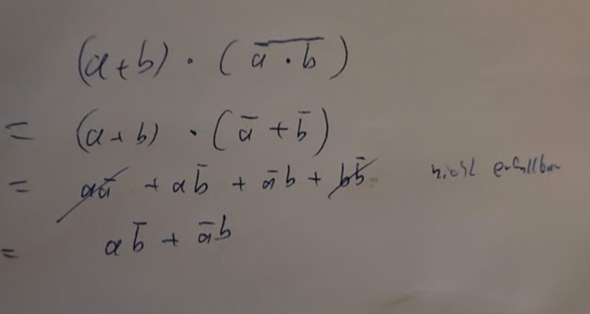
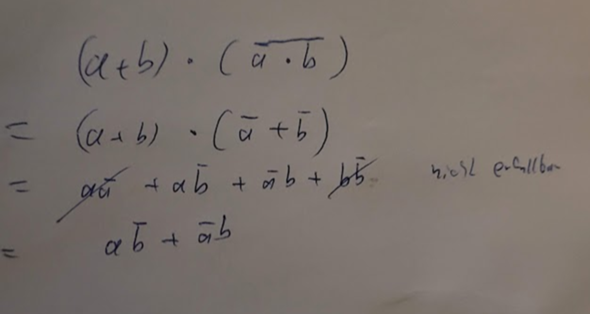
Ich ergänze gleich mal die andere Variante oben. Man kann in Kommentaren dummerweise keine Bilder einfügen.
So, habe die andere Richtung ergänzt. Problem dürfte wie gesagt aber sein, in der anderen Richtung die beiden gestrichenen - da nicht erfüllbaren - Kombis REINzukriegen.
Da inzwischen aber auch ein Mathematiker hier aufgeschlagen ist, halt Dich an den, die können sowas meist besser :-D
Danke! So hat's geklappt. Bis zu DeMorgan war ich auch noch gekommen, habe aber nicht so weit gedacht, die logischen Und/Oder als Addition bzw. Multiplikation darzustellen und mit diesen die Klammern aufzulösen.
Freut mich. Da ich selbst nicht so der große Theoretiker bin, würde mich jetzt aber doch interessieren: Wenn Du es jetzt andersrum machst, wie begründet du da das hinzufügen der zwei unmöglichen Kombis?
Habe es am Ende nicht andersrum gemacht, die eine Richtung hat für den Beweis (ging um Mengengleichheit) ausgereicht.
guck mal


Wenn dir konkret der Ansatz fehlt, würde ich vielleicht beim "Ziel" anfangen: Hier liegt ja z.B. ein Rechenschritt mit DeMorgan recht nahe. Da es sich bei DeMorgan, Distributivgesetz etc. um Äquivalenzen handelt, kannst du deinen Beweis am Ende einfach andersherum aufschreiben, als du ihn tatsächlich entwickelt hast ;)
Kann ggf. auch zunächst anders rum sein, wenn die Umformung in die eine Richtung steht, sollte es danach ja im Regelfall relativ einfach möglich sein, diese in die andere Richtung umzudrehen.