Annahme zum Spannungsteiler?
Hallo!
Ein Spannungsteiler bestehe aus 3 Widerständen R1, R2 und RL.
Wobei ja R2 || RL eigentlich ein Stromteiler ist?
Stimmt die Annahme, dass an R2 und RL immer dieselbe Spannung abfällt, aber auf Grund der Widerstandswerte unterschiedlicher Strom fließt?
Dabei immer der niedrigere Widerstand den Spannungsabfall am anderen bestimmt.
Z. B.: Ist Uq = 10V, R1= 1000Ω, R2 = 1000Ω und R3 = 0,001Ω, dann liegt an R1 quasi die ganze Spannung an, an den anderen beide quasi 0.
Liegt also immer am größeren Widerstand dieselbe Spannung an, wie am kleineren und am kleineren die Spannung im Verhaltnis R1 : (R2 || RL)?
Lg
3 Antworten
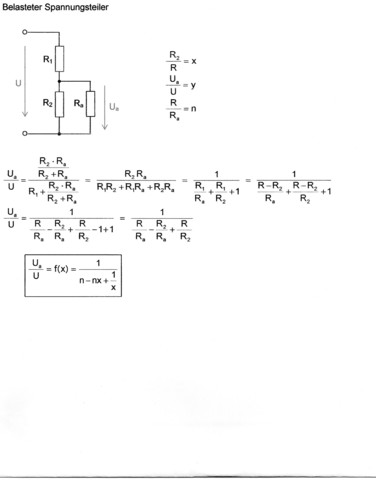
Den vollständigen Überblick über die Betriebszustände des belasteten Potenziometers erhält man im folgenden Bild.
Wenn man die Funktion Ua/U = f(x) mit dem Parameter n = R/Ra grafisch darstellt, erhält man eine Kennlinienschar, mit der sich jeder Betriebszustand grafisch darstellen lässt.
Gruß, H.
Die Potenziometerschaltung dient m.E. in erster Linie zum Einstellen einer Spannung. Dass man dabei u.a. eine Stromverzweigung nutzt, ist nebensächlich.
Natürlich wird das erwähnt. Durch eine Reihenschaltung von Widerständen teilt sich die Spannung entsprechend ihrer Widerstandswerte auf, bei einer Parallelschaltung teilt sich der Strom entsprechend auf.
Das ist im Prinzip alles, was du wissen musst, um Ströme und Spannungen zu berechnen. Selbst in sehr komplexen Netzwerken, die aus Ohmschen Widerständen bestehen.
Im Prinzip braucht man den Stromteiler um die Spannung auf 0V zu regeln, oder?
Beim unbelasteten Potenziometer ist kein Stromteiler erforderlich, um die Spannung U = 0V einzustellen. Der Stromteiler entsteht erst, wenn das Potenziometer belastet wird.
Ich weiß nicht genau, was mit unbelastetem Potentiometer gemeint ist, aber wenn R Last hinter einem Potentiometer ohne parallelen Widerstand ist, dann teilt sich ja Uq immer auf Potentiometer und R Last auf, wodurch bei Poti = 0 Ohm Uq an R Last anliegt, umgekehrt aber das Poti = unendlich Ohm haben müsste, damit 0V an R Last anliegen.
Ich vermute, dass Du die Einstellung der Spannung am Lastwiderstand mittels Potenziometer und die Einstellung der Spannung mittels Vorwiderstand nicht differenziert betrachtest. Das sind zwei verschiedene Möglichkeiten, für die die kirchhoffschen Gesetze entsprechend anzuwenden sind.
Der Lastwiderstand mit sagen wir 10MOhm liegt ja wenn das Poti auf z. B. 100.000 Ohm ist auf 0V, weil er kurzgeschlossen wird, über den Schleiferkontakt mit 0 Ohm, oder? Oder wenn das Poti auf 0 Ohm ist, dann liegt R Last auf Potential von Vcc.
Das sind die beiden Grenzfälle, wenn der Schleifer des Potis auf Anschlag, d.h., an dem einen bzw. anderen Ende des Potis steht. Dann ist entweder R1 oder R2 Null Ohm.
Bei einer Parallelschaltung von Widerständen fällt über beide parallele Zweige die selbe Spannung ab. Dies liegt daran, dass deren Anfangs- und Endklemmen auf dem jeweils gleichen Potential liegen und somit die Potentialdifferenz (Spannung) die selbe ist. Dieser Umstand findet sich in der sogennanten "kirchhoff´schen Maschenregel" wieder.
Für deinen speziellen Fall folgt damit:
U2 = UL
Und mit Quellspannung Uq folgt damit:
U1 = Uq * R1/(R1 + (R2 II RL ))
U1 + U2 = Uq
U1 + UL = Uq
U2 = UL = Uq = (R2 II RL)/( R1 + (R2 II RL ))
Zu den Strömen in lässt sich sagen wegen:
U2 = UL
folgt mit dem ohmschen Gesetz:
R2*I2 = RL*IL
Und damit ist das Verhältnis beider Ströme gegeben zu:
I2/IL = RL/R2
Das heißt, das Potential unterhalb bzw. nach R1 wird festgelegt durch alle 3 Widerstände?
Ja, und durch den Strom. Aber der ergibt sich ja automatisch durch die Widerstände und die Gesamtspannung.
Ich nehme mal an R3 und RL sollen das Gleiche bedeuten.
An zwei parallelen Elementen ist immer die gleiche Spannung.
Bei so extremen Fällen wie R2=1000 Ω und R3 = 0,001 Ω stimmt die Annahme ungefähr, dass der niedrigere Widerstand den Spannungswert bestimmt. Aber ansonsten musst du den Ersatzwiderstand in einer Parallelschaltung berechnen um eine Aussage über die Spannung zu sagen. Sicher ist nur, dass die Spannung an R2 und R3 gleich ist. Egal, wie die Zahlenwerte sind.
Also bestimmt jeder Widerstand die Spannungsverhältnisse in der jeweiligen Masche immer?
Ja, nur unendlich große oder unendlich kleine Widerstände können in gewisser Weise (je nach speziellem Fall) vernachlässigt werden. Ansonsten müssen alle Widerstände zur Berechnung berücksichtigt werden.
Warum wird in diversen Lehrmedien nie erwähnt, dass es sich gewissermaßen um einen Spannungs- und Stromteiler handelt?