Äquivalenz nachweisen DFA?
Hallo Leute ich bräuchte Hilfe bei folgender Aufgabe:
Zeigen Sie fur jedes Paar {q, p} von Zuständen des DFA M′ ,dass q und p nicht äquivalent sind.
Das hier ist das DFA:
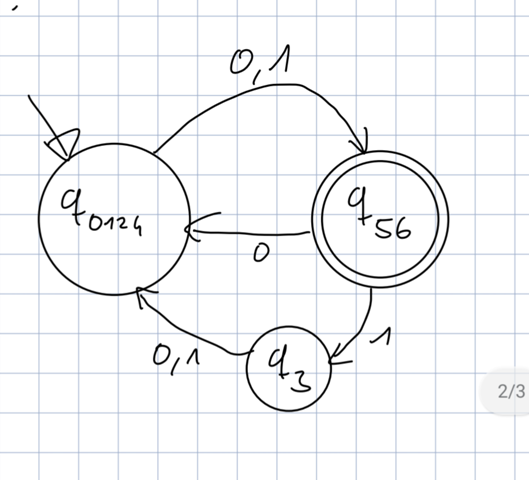
Ich habe schon ein Teil gemacht, bin mir aber nicht sicher ob das gemacht werden kann. Noch dazu finde ich es nicht formal so schön:

1 Antwort
Also es sollte eigentlich ausreichen, wenn du für jedes paar eine Zeichenkette findest, sodass du einmal beim Akzeptierenden Zustand landest und ein Mal nicht, wenn du jeweils an einem der beiden zustände anfängst und dann der Zeichenkette folgst.
Zum Beispiel:
bei q_0124 und q_56:
Wähle einfach das Leere Wort, du bleibst dann jeweils bei dem Zustand stehen. Da q_0124 nicht akzeptierend ist, q_56 hingegen schon, sind die beiden nicht äquivalent.
Besser gesagt, du musst immer nur ein Gegenbeispiel finden, um zu zeigen, dass die nicht äquivalent sind.