Warum ist die Wurzel von 0,04 die 0,2? Die gezogene Wurzel kann doch nicht größer sein als die Wurzelzahl.

Überleg Dir mal, was 0,2 eigentlich bedeutet ...

Als Bruch geschrieben, ist 0,2 = 1/5.

Und 0,2² ist dann also (1/5)² = 1/5 * 1/5, oder anders gesagt: 1/5 von 1/5 - dass ein Bruchteil von etwas kleinem noch kleiner ist, dürfte doch einleuchten, oder?

Und wenn durch Quadrieren einer Zahl zwischen 1 und 0 das Ergebnis kleiner wird, dann muss logischerweise bei der Umkehrung, dem Wurzelziehen, das Ergebnis größer werden ...

naja was ist denn 0,2 mal 0,2? richtig 0,04 und damit ist 0,2 die wurzel von 0,4.

wenn du eine zahl zwischen 0 und 1 mit einer anderen zahl multiplizierst, ist das produkt nunmal kleiner als die andere zahl. hier nimmst du sie eben mit sich selbst mal und damit wird das ergebnis noch kleiner

Du zeigst normales menschliches Verhalten und denkst linear.

Die Wurzelfunktion sqrt(x)  ist aber eine nichtlineare Funktion:

Wenn man doppelt so viel reinsteckt, kommt nicht doppelt so viel raus!

Hier ist das Ergebnis zufällig im Kopf lösbar, denn 0.2 * 0.2 =0.04

http://www.gerdlamprecht.de/Liniendiagramm_Scientific_plotter.htm

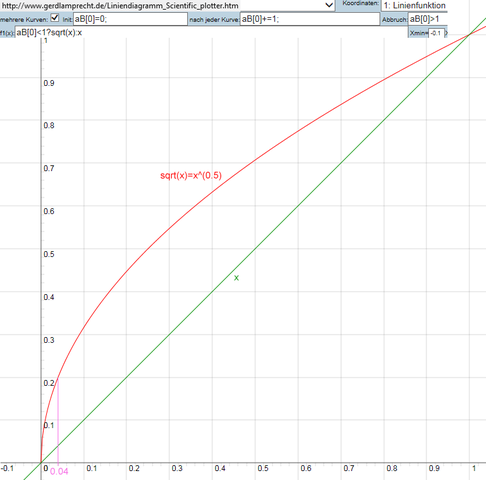
Siehe Bild rot sqrt und grün linear

Aber allg. gilt

Wurzel(x)=sqrt(x)=x^(1/2)=e^(log(x)/2)=exp(log(x)/2)

Viele verstehen auch nicht, warum man die Wurzel aus 0.05 nicht mit endlich vielen Stellen angeben kann.

exp(log(0.05)/2)

ist

für x<1:

429/2048+(3003 x)/2048-(3003 x²)/2048+(3003 x³)/2048-(2145 x^4)/2048+(1001 x^5)/2048-(273 x^6)/2048... bis in alle Ewigkeit

ergibt für x=0.05 ->  0.22360679774997896964... unendlich viele weitere Stellen ohne Periode!!

Die gezogene Wurzel kann doch nicht größer sein als die Wurzelzahl....

...doch kann sie. Niemand hat jemals behauptet, daß die Wurzel aus einer Zahl stets kleiner sein muss, als die Zahl selber.

Du selber hast gerade eine Beispiel für diesen Fall aufgezeigt. ;-)

doch, rechne mal 0,04 mal 0,04. kommt was kleineres raus. Wurzeln ist das Gegenteil vom Quadrieren also kommt was grösseres raus