Wie soll ich diese Rechenmauer lösen?
Hey Leute. Ich sitze jetzt seit einer Stunde an diesen beiden Aufgaben, aber ich kann sie einfach nicht lösen. Ich soll die beiden Pyramiden erstmal mit den benötigten X und Y einfüllen, und danach nocheinmal mit den benötigten Zahlen.. Kann mir jemand helfen?
3 Antworten
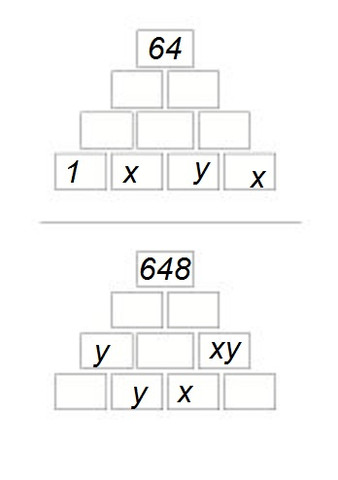
64
a b
c d e
1 x y x
c = 1+x, d=x+y, e=x+y
a = c+d = 2x+y+1
b = d+e = 2x+2y
64 = a+b = 4x+3y+1
und dann kannst du dir aussuchen, was du für x und y nimmst (z.B. x=0 und y=(64-1)/3 = 63/3 = 21)
genauso geht das bei der anderen, such dir dann einfach schöne Zahlen für x und y, oder vllt ist es ja sogar eindeutig
Nehmen wir mal das erste.
Mir scheint, da soll dividiert werden, also von unten her multipliziert. Rechne ich von unten nach oben, sind in den drei Feldern die Terme
x xy xy
Darüber nur noch:
x²y (xy)²
Daher ist x^4 * y³ = 64
Bei der Größenordnung wird es ohne Bruch nicht gehen.
Nun ist 1/2 nicht gut, wie man schnell sieht, daher y = 1/4 und y³ = 1/64
Um dann 64 herauszubekommen, kann x^4 nur noch 4096 sein, also x = 8.
Tatsächlich ist 8^4 * (1/4)³ = 64
Jetzt brauchst du nur noch die ausgerechneten Terme einzufügen.
Wenn noch Fragen sind, schreib einen Kommentar.
Bei der zweiten musst du mit Multiplikation arbeiten. Links unten gehört eine 1 hin, da 1*y = y. Rechts unten gehört das hin, was mit x multipliziert XY ergibt.
Am Ende machst du eine Primfaktorzerlegung, dann weißt du welche Zahl was ist.