Wie kann man resultierende Kraft berechnen?
Servus!
Kann jemanden mir bei der Lösung dieser Frage helfen?
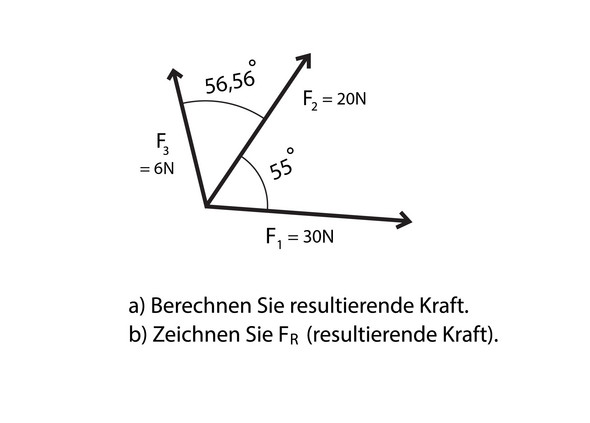
Ich danke Ihnen voraus.
3 Antworten
zeichnerisch geht das am einfachsten.
Alle 3 Kräfte aneinanderreihen
F2 parallel verschieben und mit den Anfang an die Spitze von F1
Dann F3 parallelverschieben mit den Anfang an der schon parallelverschobenen Kraft F2 legen.
Resultierende Kraft ist dann die Verbindung von Anfang F1 zu Spitze F3.
Rechnerisch.
1) ein x-y-Koodinatensystem am Anfang von F1 legen
2) die Kräfte in ihre Komponenten zerlegen , in y- Richtung und x- Richtung
3) Die Summe der Kräfte in y- Richtung bilden und die Summe der Kräfte in x-Richtung bilden
4) Die resultierende Kraft ist dann Fres=Wurzel(Fy^2+Fx^2)
Hinweis . F3x=cos(68,44°)*6 N=- 2,206 N zeigt in "negativer" x-Richtung
b=68,44°=180°-55°-56,56°=68,44°
Hier die Werte:
F1x=30 N und F1y=0
F2x=cos(55°)*20N=11,47..N F2y=sin(55°)*20N=16,38..N
F3x=cos(68,44°)*6N=-2,205N und F3y=sin(68,44°)*6N=5,58N
Den Rest schaffst du selber und hat schon Geograph gemacht.
Kräfte in Komponenten zerlegen und addieren:
Da in der Aufgabe kein Koordinatensystem vorgegeben ist, darf man dieses frei wählen. Deshalb die Anmerkung "Mit x-Achse in Richtung F1".
Lege diese Kräfte in den Ursprung eines Koordinatensystems.
Dann jede Kraft in x-y Komponente aufteilen
nun alle x und alle y addieren und du kriegst als summe x bzw summe y die Komponenten der Resultierenden
Zeichnen: alle Pfeile aneinander hängen. vom Anfang des 1. Pfeils bis zur Spitze des 3. Pfeils zeichnest du die Resultierende
Achtung... wenn ich es recht sehe, dann liegt F1 NICHT horizontal, hat also eine y-Komponente. Du hast die Summierung in einem gedrehten KO-System vorgenommen