Wie geht Satz des Pythagoras?
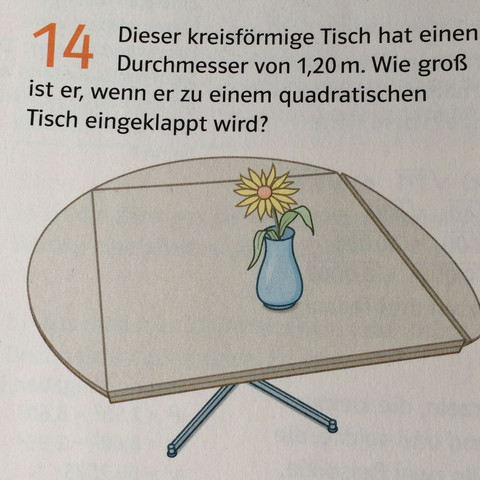
Wir haben gerade in Mathe Satz des Pythagoras und wir haben jetzt eine Aufgaben aufbekommen, die ich einfach nicht verstehe. Falls Sie mir jemand erklären kann, dann bitte mit Rechen weg
7 Antworten
Wie "groß" er ist, hängt davon ab, woran man das misst: An der Diagonale, dass wird es nicht sein, da das trivial wäre (genau wie vorher, d=1,20m.
Es wird also entweder die Seitenlänge s oder die Fläche A gemeint sein. A ist natürlich einfach s².
Weil man den Satz des Pythagoras benutzen soll, braucht man ein rechtwinkliges Dreieck, und das findet man in zwei Seiten des quadratischen Tisches und der Diagonalen.
Die - gesuchten - Katheten sind gleich, also sind es auch ihre Quadrate.
Deren Summe und damit das Doppelte von einem, also 2s², ist das Quadrat der Hypotenuse, also d², und damit ergibt sich
s² = A = ½d² = ½•1,44m² = 0,72m².
Daraus ergibt sich s zu etwas weniger als 0,85m.
Der Satz des Pythagoras lautet a²+b²=c².
Anders als sonst braucht man hier ausnahmsweise nicht den Radius, sondern den ganzen Durchmesser. Wenn man sich ein halbes Quadrat beguckt, gilt nämlich nach Pythagoras:
2a² = d² Die Seiten des Quadrats sind die Katheten,
die Diagonale ist die Hypotenuse und ebenso lang wie
der Durchmesser des Kreises, also
a² = d²/2 | √
a = √(d²/2)
a = √(1,44/2)
a = 0,85 m (gerundet)
Eigentlich habe ich viel zu weit gerechnet. Denn es sollte ja die Größe des Quadrats bestimmt werden. Die war schon da mit
a² = d²/2 = 0,72 m²
a = 0,85 m
ist dann die Seitenlänge dieses quadratischen Tisches.
Mit dem Satz des Pythagoras ermittelt man die Größe eines Dreiecks mit einem rechten Winkel.
a^2 + b^2 = c^2
In einem Rechtwinkligen Dreieck sind die beiden Kathetenquadrate gemeinsam so groß wie das Hypothenusenquadrad.
Also so musste ich es damals lernen.