Welcher Unterschied besteht hier zwischen dem größten/kleinsten durschnitt und der Standard abweichung?
An alle Statistik Liebhaber, wie würdet ihr mit dieser Frage umgehen. Bin grad ein wenig überfragt, was man bei diesen Daten noch diskutieren könnte.
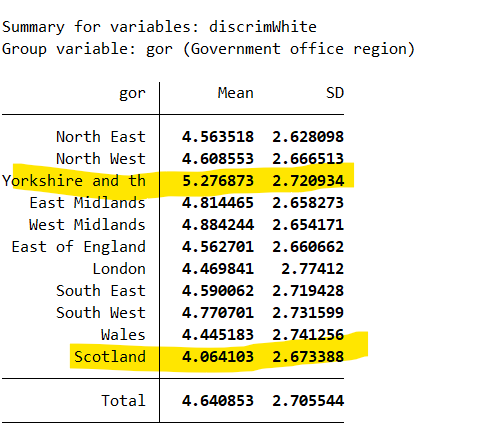
hier noch die gesamte frage
"Discuss the difference between the standard deviation of the region with the highest mean level of perceived discrimination against and the region with the lowest mean level of perceived discrimination against."
2 Antworten
das arithmetische Mittel (Durchschnitt) bedeutet, dass man alle Werte zusammenzählt und durch 2 teilt.
Der Median bedeutet, dass der mittlere Wert genommen wird.
Zum Beispiel die Liste {1; 3; 6}
- der Durchschnitt ist 5, da (1 + 3 + 6) / 2 = 10 / 2 = 5
- der Median ist 3, da 3 in der Mitte der (geordneten) Liste ist
(wenn es eine gerade Anzahl von Werten gibt, nimmt man für den Median den Durchschnitt von den zwei mittleren Werten)
hoffentlich hilft dir das weiter!
Es geht darum, dass Du zeigst, dass Du verstehst, was die Standardabweichung bedeutet. Die Standardabweichung ist in beiden Gegenden mit 2.72 bzw. 2.67 recht ähnlich. Es gibt auch Hypothesentests mit denen man diesen Unterschied auf Signifikanz testen könnte (z.B. F-Test für Varianzen). Aber mann schon anhand der Zahlen vermuten, dass das kein signifikanter Unterschied ist. Und wenn die beiden Werte ähnlich sind, bedeutet das: auch wenn die Regionen sich vom Mittelwert unterscheiden, scheint die Streuung im perceived level of discrimination in beiden Regionen recht ähnlich zu sein. Das heißt: es scheint eher nicht so zu sein, dass die Einschätzungen in einer Region stärker auf der Skala streuen als in der anderen Region. Rein numerisch ist in Yorkshire die Streuung leucht höher als in Scotland, aber man kann Zweifel daran äußern, ob das ein signifikanter Unterschied ist.