Welche Funktionen sind nicht unendlich oft differenzierbar?
Die meisten Funktionen sind ja unendlich oft differenzierbar (auch wenn dann mal Null rauskommt). Welche Funktionen sind es dann nicht?
1 Antwort
Viele Funktionen sind an bestimmten Stellen nicht unendlich oft differenzierbar oder auch gar nicht differenzierbar Oft enthalten solche Funktionen einen Betrag beziehungsweise sind in verschiedenen Teilbereichen unterschiedlich definiert. Die meisten verwendeten stetigen Funktionen sind in Teilbereichen unendlich oft differenzierbar. Funktionen, die an einer Stelle nicht stetig sind, sind auch an dieser Stelle nicht differenzierbar. Funktionen, die an keiner Stelle stetig sind, sind auch an keiner Stelle differenzierbar. Ist die Ableitung einer Funktion an einer Stelle nicht stetig, dann ist die Funktion an dieser Stelle auch nicht weiter differenzierbar.,
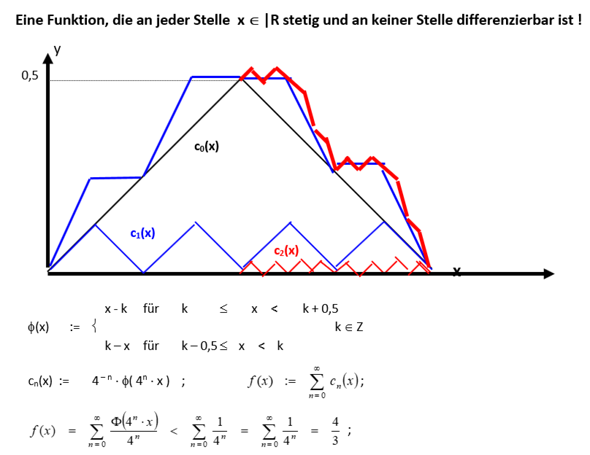
Ungewöhnliche Funktionen sind solche, die zwar an jeder Stelle eines Intervalls stetig aber an keiner Stelle differenzierbar sind.
Beispiel aus meinem alten Unterrichtskonzept:

Den zugehörigen Beweis habe ich hier jetzt nicht abgebildet.
Wenn man unterstellen würde, dass die Funktion f(t) = s(t) die Zeit-Weg-Funktion einer Bewegung wäre, dann hätte diese an keiner Stelle eine eindeutige Geschwindigkeit.