Was ist der Unterschied zwischen beiden Schreibweisen (Mathe, Stochastik)?

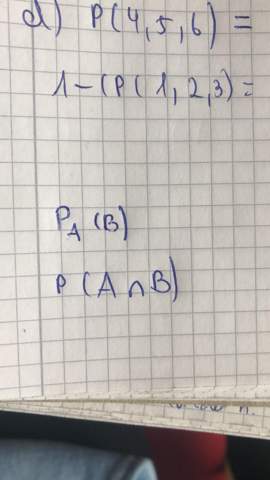
2 Antworten

Vom Fragesteller als hilfreich ausgezeichnet
davebot
19.10.2019, 12:10

So viel ich weiß bedeutet die erste Schreibweise, dass Aussage A schon erfüllt ist und nur noch die Wahrscheinlichkeit gesucht wird, dass Aussage B richtig ist.
Als Beispiel:
A: alle Brillenträger
B: alle Frauen

Die erste schreibweise sucht unter allen Brillenträgern die frauen raus. Zwar werden dort natürlich nur alle Frauen rausgesucht, die eine brille tragen, jedoch ist die Wahrscheinlichkeit höher als bei der 2. schreibweise, da bei der 1. schreibweise die Personen ohne brille schon im Vorfeld rausgefiltert werden.
Eine Wahrscheinlichkeit ist ja immer nur "gewünschtes Ergebnis"/"mögliche Ergebnisse".
Doch "mögliche Ergebnisse" im Nenner ist bei der ersten schreibweise kleiner, da sämtliche Ergebnisse, die Personen ohne Brille beinhalten, gar nicht möglich sind. Schließlich ist die Bedingung im Vorfeld ja schon, dass die Aussage "trägt brille" wahr ist.
Also kurz gefasst: beide Schreibweisen suchen zwar die schnittmenge zwischen A und B raus, jedoch tut es die erste schreibweise in einer kleineren "gruppe"
Woher ich das weiß:Studium / Ausbildung – Ehemaliger Mathestudent & War schon immer ein Zahlenfreund
verreisterNutzer  19.10.2019, 12:14

So kann man es ungefähr ausdrücken. Am besten illustriert es dieses Bild:

http://www.rither.de/images/mathematik/stochastik/bedingte-wahrscheinlichkeit/bedw_a_und_b.jpg (Schnittmenge)

und dieses:

http://www.rither.de/images/mathematik/stochastik/bedingte-wahrscheinlichkeit/bedw_b_unter_bedingung_a.jpg (B unter der Bedingung A)

Als Randbemerkung: Mich stört an der derzeitigen Mathematikdidaktik in Schulen vor allem der mangelnde intuitive Zugang zur Stochastik. Es wird immer schlimmer.

1
verreisterNutzer
19.10.2019, 12:06

In dem einen Fall, wird die Wahrscheinlichkeit von B unter der Bedingung von A betrachtet, d.h. im Falle, dass Wahrscheinlichkeit A schon eingetreten IST!

Im zweiten Fall wird dagegen die Wahrscheinlichkeit betrachtet, in der A und B gemeinsam, d.h. gleichzeitig stattfinden. (A und B)