Wachstumsprozesse modellieren?
Ich versteh die Aufgabe nicht, helppp!!!!
2 Antworten
Wie sieht bei Euch eine Funktionsgleichung für einen exponentiellen Zu-/Abnahmeprozess aus? Es gibt da (mindestens) zwei Varianten. Ich gehe mal von der Form f(t) = A · e^(c·t) aus, das ist die gebräuchlichste. Dabei steht t für die Zeit in Jahren, f(t) für den Bestand nach t Jahren.
Du hast keine Ausgangsmenge vorgegeben; statt dessen ist von Prozentwerten die Rede. Daher setze ich A = 100 (für 100 %).
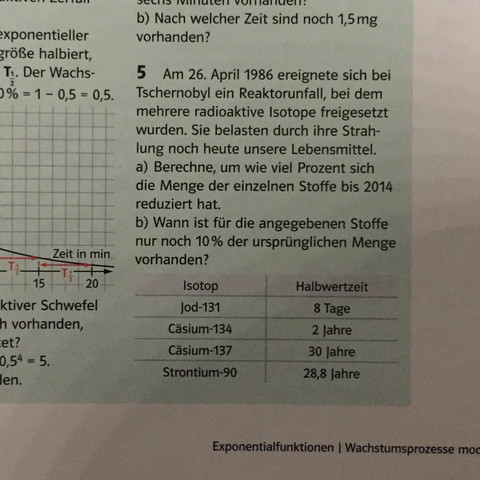
Nun musst Du für jeden einzelnen Stoff jeweils die Zerfallskonstante c berechnen. Dies geht mit der vorgegebenen Habwertzeit.
Beispiel Cäsium-134:
50 = 100 · e^(c·2)
Diese Gleichung nach c auflösen, und Du kennst das Zerfallsgesetz für Cäsium-134. Jetzt kannst Du Dich an die eigentliche Bearbeitung der Aufgaben a) und b) machen.
Bei a) setzt Du für t die entsprechenden Wert für t ein (vgl. UlrichNagel), bei b) ist f(t) vorgegeben: Wert einsetzen und die Gleichung nach t auflösen.
Soweit klar?
Du hast 27 Jahre und 245 Tage für den Verfallsprozess! Nun schau dir an, was Halbwertszeit bedeutet und nun kannst du mit den Angaben rechnen!