Vorzeichen von Rotationsmatrix stimmt nicht, obwohl in allen Quellen im Internet diese Lösung existiert.. ?
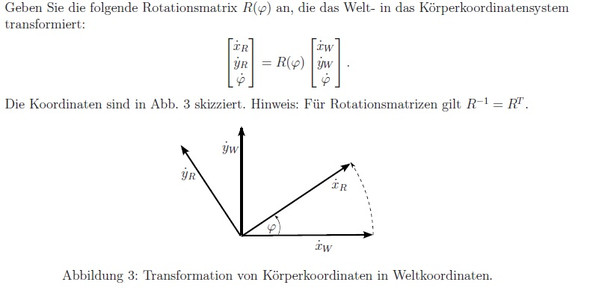
also ich soll die Rotationsmatrix in Bild 1 bestimmen und das habe ich in Bild 2 gemacht...
die Lösung mit genau diesen Vorzeichen finde ich in allen Internetquellen für den Fall, dass gegen den Uhrzeigersinn gedreht wird und das ist ja hier auch der Fall...
wenn ich aber nun z.B. für Phi 90° einsetze, kommt z.B. für xR= -yW raus und das ist ja nach der Abbildung ganz offensichtlich das falsche Vorzeichen, denn xR tritt ja dann an die Stelle von xW!
Wo ist der Fehler?
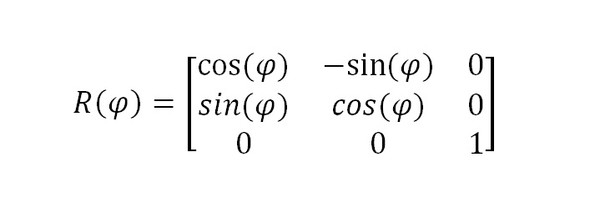
2 Antworten
Ohne mich in dieses konkrete Beispiel einzudenken: Die Frage ist, ob die die Koordinaten oder die Basisvektoren transformierst, diese beiden Transformationen sind genau invers zueinander.
Nein, nur bei den sin (nutze, dass R^-1 = R^T).
Stelle dir einen Vektor, der von der Sonne zum Alpha Centauri zeigt. Dieser Vektor hat eine ganz klare physikalische Bedeutung und seine Richtung ist fix. Nun können wir diesen Vektor aber in unterschiedlichen Koordinatensystemen darstellen. In einem KoSy zeigt er vielleicht entlang der x-Richtung, in einem anderen entlang der y-Richtung.
Um den Vektor von einem ins andere KoSy zu überführen, kann man eine Rotationsmatrix verwenden. Sie verändert sowohl die Basisvektoren als auch die Komponenten des Vektors, allerdings genau so, dass der Vektor als ganzes wieder der gleiche ist.
Die angegebene Drehmatrix beschreibt die aktive Drehung eines Punktes.
Das Koordinatensystem bleibt damit gleich, nur der Punkt verändert die Koordinaten.
Die Drehrichtung erfolgt entgegen dem Uhrzeigersinn und stimmt auch für 90 Grad. Auf zwei Koordinaten beschränkt gilt
xR = x * cos(w) - y * sin(w)
yR = x * sin(w) + y * cos(w)
Für w = 90
xR = - y
yR = x
Der Punkt [1,0] z.B. wandert damit nach [0,1]
Der Punkt [0,1] z.B. wandert damit nach [-1,0]
(wie zu erwarten).
Aber da hier ja das Koordinatensystem transformiert werden soll, ist die passive Drehung die Richtige, oder?
Das geht aus der Aufgabe nicht klar hervor, vor allem die Vektordarstellung sieht wie eine aktive Drehung aus.
Die passive Drehung ergibt sich dann aus der inversen Drehmatrix.
Die Drehmatrizen im Internet sind meistens aktive Drehungen und deshalb richtig.
vielleicht hilft die Anwendung weiter: Es handelt sich um einen Roboter mit 3 Antrieben, der sich kreisförmig drehen kann und ein eigenes Koordinatensystem hat
die Gleichungen für die Antiebe sind in Relation mit dem eigenen Koordinatensystem gegeben und für die Zustandsdarstellung des Roboters braucht man das "normale Koordinatensystem"
aber was macht das denn für einen Unterschied? Also einfach bei jedem sin und cos-Ausdruck das Vorzeichen tauschen?