Verstehe den Unterschied zwischen Algebra und Arithmetik nicht?
Hallo,
leider verstehe ich nicht die beiden Disziplinen, wenn es konkreter wird. Als Beispiel die grundlegenden Rechengesetze Assoziativgesetz, Kommutativgesetz und Distributivgesetz.
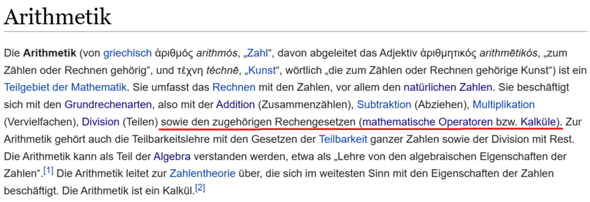
Daraus entnehme ich, dass die Arithmetik sich mit diesen zugehörigen Rechengesetzen (Assoziativgesetz, Kommutativgesetz und Distributivgesetz) unteranderem befasst.
Wenn ich mir jedoch das hier durchlese:
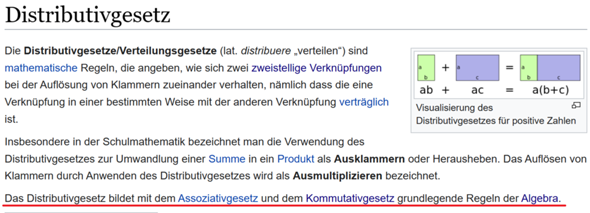
Also beschäftigt sich auch die Algebra mit Assoziativgesetz, Kommutativgesetz und Distributivgesetz ?
Da frage ich mich, in wie fern jetzt bezogen auf Assoziativgesetz, Kommutativgesetz und Distributivgesetz sich die Arithmetik von der Algebra unterscheidet? Ich verstehe das leider nicht.
Und noch eine Frage:
sind das hier algebraische Darstellungen oder arithmetische Darstellungen?
Sagt man also dazu arithmetische Ausdrücke oder algebraische Ausdrücke?
2 Antworten
Verstehe den Unterschied zwischen Algebra und Arithmetik nicht?
Algebra und Arithmetik teilen sich sehr viele Eigenschaften.
In seinen fundamentalsten Grundzügen kann man wohl sagen, dass Algebra die Theorie der Verknüpfungen mathematischer Strukturen ist, also das was du z.B. nutzt wenn zwei Saschen vergleichst (größer, kleiner, gleich, ungleich, mächtiger, schmächtiger, gleich mächtig, ...).
Unter Arithmetik wird hingegen das Rechnen an sich verstanden.
Das heißt, dass das was du arithmetisches mit Algebra Verknüpfst.
Z.B.
2 + 2 = 4 eine Operation zwischen zwei natürlichen Zahlen und gehört somit zur Arithmetik.
2 + x = 2 * 2 ist eine Gleichung, welche eine Verknüpfungen mathematischer Strukturen ist, weswegen es der Algebra angehörig ist, aber enthält natürlich auch die Operation 2 * 2 unter natürlichen Zahlen, was der Arithmetik angehört.
Der Übergang von Arithmetik und Algebra, weswegen sie beide oft als gleichwertig oder sogar als Synonym füreinander betrachtet werden, was zwar wie ich finde etwas stumpf verallgemeinert ist, doch es für die Schulmathematik genügend beschreibt.
Also beschäftigt sich auch die Algebra mit Assoziativgesetz, Kommutativgesetz und Distributivgesetz? Da frage ich mich, in wie fern jetzt bezogen auf Assoziativgesetz, Kommutativgesetz und Distributivgesetz sich die Arithmetik von der Algebra unterscheidet?
Damit beschäftigt sich Algebra, da es schließlich Verknüpfungen mathematischer Strukturen sind.
Diese algebraischen Strukturen werden aber auch in der Arithmetik genutzt.
In der Algebra heiß es gemäß Distributivgesätz z.B.
a * (b + c) = a * b + a * c, was eindeutig eine algebraische Struktur ist, denn ich sehe hier keine Zahlen, sondern Variablen.
Dieses aus der Algebra stammende Gesetz können wir jetzt aber auch auf den arithmetischen Ausdruck anwenden:
2 * (4 + 1) = 2 * 4 + 2 * 1
sind das hier algebraische Darstellungen oder arithmetische Darstellungen?
Das sind algebraische Darstellungen, wegen der Verknüpfung.
Eine einfache verallgemeinerte Merkhilfe ist, dass wenn im Ausdruck Variablen irgendwie in Verbindung stehen, dann ist es ein algebraischer Ausdruck.
Stehen da hingegen nur Zahlen und Rechenoperatoren in Verbindung ist es ein arithmetischer Ausdruck.
"Im Gegensatz zur Arithmetik treten in der elementaren Algebra neben Zahlen und den Grundrechenarten auch Variablen auf. Im Gegensatz zur abstrakten Algebra werden in der elementaren Algebra keine algebraischen Strukturen, wie Vektorräume, betrachtet." - Quelle: Wikipedia oder auch diese ominöse Seite
Sagt man also dazu arithmetische Ausdrücke oder algebraische Ausdrücke?
Ja... Warum nicht...
Wenn du dich weiter einlesen willst, kannst du aber auf die andere Frage auf gutefrage gehen, die das "gleiche" fragt...
a * (b + c) = a * b + a * c, was eindeutig eine algebraische Struktur ist, denn ich sehe hier keine Zahlen, sondern Variablen.
Beispiel: Mengenlehre, Aussagenlogik, Matrizen
Hast du
Die Arithmetik kann als Teil der Algebra verstanden werden, etwa als „Lehre von den algebraischen Eigenschaften der Zahlen“
gelesen und verstanden? Du konstruierst ein
Ach bei DerRoll kannst du dir sicher sein, dass er die Antwort kennt.
Danke dir. Leider habe ich nicht verstanden, was man mit "algebraischen Eigenschaften der Zahlen" genau meint?
Könntest du vielleicht auch auf die anderen Fragen eingehen, die ich da weiter unten stellte, ob es sich bei den gegeben Darstellungen um algebraische oder arithmetische Darstellungen handelt?