Unendlicher Widerstand bei idealen Stromquellen?
Wie kann ich das eigentlilch verstehen? Es kann ja kein Strom fließen wenn ein zu großer innenwiderstand vorhanden ist oder? Und wieso sollte der Innenwidertand unendlich groß sein?
5 Antworten
Eine sehr berechtigte Frage! Kompliment!. Du willst also nicht nur rechnen, sondern auch VERSTEHEN!. Da hilft nämlich so ein Ersatzschaltbild mit dem Symbol einer idealen Stromquelle nicht weiter. Das Wort "ideal" sagt es ja schon: Sowas gibt es gar nicht in Realität!.
Wir müssen unterscheiden zwischen Quellen für Gleichspannung/Gleichstrom und Quellen, die gegenüber Änderungen unempfindlich sein sollen und somit einen sehr großen DYNAMISCH-DIFFERENTIELLEN Innenwiderstand haben.
Fall 1: Es gibt keine "Stromquelle", sondern nur Spannungsquellen. Einfache Vorstellung: Batterie oder Akku mit Spannung Uo. Wenn man vor den Verbraucher mit dem ohmschen Eingangswidersand Re einen sehr großen Vorwiderstand Rv>>Re schaltet, ist der fließende Strom nahezu (aber nie 100%-ig) unabhängig von Re und primär von Re und Uo. Bei Rv unendlich (Stromkreis offen) fließt natürlich gar kein Strom mehr.
Fall2: Gleiche Anordnung - nur ist der Vorwiderstand jetzt kein simpler Ohm-Wderstand mehr, sondern eine Aktiv-Schaltung (Transistor oder OPV) mit einem Widerstand Rv, der veränderlich ist und gesteuert werden kann. Es gibt jetzt also nicht nur einen statisch festen (man sagt: statischen) Vorwiderstand, sondern auch den differentiellen (Änderungs-)Widerstand, der mit einem kleinen Symbol rv beschrieben wird.
Zur Erklärung: Denke z.B. an die Diode, bei der der statische Widerstand Rd=Ud/Id anders ist als der dynamische rd=d(Ud)/d/Id), der die Steigung der Tangente an den durch Ud und Id beschriebenen Arbeitspunkt angibt.
Durch geschickte Rückkopplung kann man nun dafür sorgen, dass bei Änderung der Last (z.B. mit kleinerem Eingangswiderstand Re, also negativer Änderung) der Innenwiderstand der Quelle sich entgegengesetzt verhält und fast um den gleichen Wert größer wird (also positiver Änderung). Als Ergebnis bleibt die Summe der Widerstände konstant (die Summe der Änderungen ist im Idealfall Null) und der Strom bleibt praktisch konstant.
Kurzform der Antwort:
Das ohmsche Gesetz gilt nur für Ohmsche (lineare) Elemente (Verbraucher).
Eine Quelle ist kein Ohmsches Element. Schon gar nicht die idealen Quellen!
Sonst müsste dich die ideale Spannungsquelle ebenso stören: Über dem 0-Ohm-Innenwiderstand kann ja auch gar kein Spannungsabfall herrschen...
Das mit dem Innenwiderstand ist somit eine Modellvorstellung, die uns hilft, die Phänomene ausserhalb der Quelle zu erklären. (Bei der Spannungsquelle liegt er ja in Serie, bei der Stromquelle parallel zur "Ur"-Quelle.
Schon ein simpler Schalter ist kein Ohmsches Element.
Und vielleicht hilft gerade der (ideale) Schalter als Bild für die Quellen:
- Ein geschlossener Schalter hat null Ohm, null Spannungsabfall und irgendeinen Strom. 0 Ohm = 0 Spannung durch x Strom , naja, geht noch knapp, aber x (Strom) kann beliebig sein. Ist also sicher nichts lineares.
- Ein offener Schalter hat unendlich Ohm, maximalen Spannungsabfall und null Strom. Unendlich Ohm = x Spannung durch 0 Strom. Nicht definiert, Spannung beliebig. Nichts lineares
Bei einer idealen Stromquelle soll der strom nicht von dem widerstand der last abhängen.
Bedeutet der Innenwiderstand muss Unendlich hoch sein, damit der widerstand der last nicht mehr relevant ist.
Bei einer idealen Stromquelle hast du dann immer einen Stromfluss von z.B. 1A.
Der Innenwiderstand, und der widerstand der last, spielt für den Strom keine rolle, es ist immer 1A.
In der praxis ist der Innenwiderstand natürlich nicht Unendlich, und je höher die Spannung steigen muss für deine 1A, desto mehr fällt der Strom ab, sonst würde die Spannung ja in das Unendliche steigen. Da braucht man dann irgendetwas zur Regulierung.
Das würde ja aber bedeuten, dass da kein Strom mehr fließt oder?
Eine ideale Spannungsquelle hat 0 Ohm Innenwiderstand.
Eine Stromquelle dagegen unendlichen Innenwiderstand.
Aber wieso hat der ideale stromquelle eine unedlich hohen Innenwideestand?
Hmmn, eigentlich brauchst du dir das Ersatzschaltbild einer Stromquelle angucken. Vermutlich hast du die falsche Schaltung im Kopf, kann das sein?
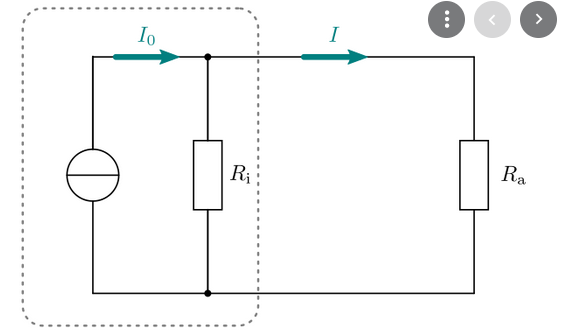

Na ja......denk mal etwas weiter. Wie stellst Du Dir denn die REAISIERUNG des Symbols der Stromquelle vor? Es gibt nämlich gar keine Stromquellen - das ist bloß der Name, den wir so im üblichen Sprachgebrauch benutzen, für eine Spannnungsquelle mit enem sehr großen Innenwiderstand - und schon bist Du wieder bei Deinem Verständnisproblem gelandet.
Und Du hast völlig recht - eine Batterie oder Akku mit einem unendlich großen Vorwiderstand (also offener Stromkreis) kann keinen Strom liefern. Ich ab dazu noch mal eine separate Antwort hier geschrieben...
Ich glaube nicht, dass deine Präzisierung weiterhilft.
Der Innenwiderstand einer Stromquelle ist eben kein "Vor"widerstand, sonden ein Parallelwiderstand. Die Spannung einer idealen Stromquelle ist nur definiert durch den Verbraucher (oder die physischen Grenzen der realen Quelle; genau wie umgekehrt der Strom einer idealen Spannungsquelle).
Komisch - der Fragesteller hat sich aber bedankt und die Antwort positiv gewertet. Aber: Deine "Präzisierung" verwechselt Modell mit Realität. Nur dann, WENN Du das Symbol einer idealen Stromquelle verwendest, wird ein vorhandener Innenwiderstand als Parallel-Element dargestellt. Das ganz ist aber ein Rechenmodell - nichts anderes! Und die Vorstellung mit Parallelwiderstand gegen unendlich hilft ja nun wirklich nicht weiter: Dann bleibt eine ideale Stromquelle übrig, die es gar nicht gibt in Realität. Weißt Du denn überhaupt noch, was der Fragesteller wollte? Deine Antwort müsste logischerweise lauten: Doch, auch bei Ri gegen unendlich fließt ein Strom. Und das ist in der Realität schlicht FALSCH (da es keine idealen Quellen gibt),
du scheinst ja immer genau zu wissen, was der Fragesteller möchte.
Deshalb hast du auch so viele tolle Bewertungen. Weiter so.
Er fragte schon im Titel nach der IDEALEN Quelle und der (Modell- JA!)-Vorstellung eines unendlichen Widerstands.
Mit Deinen unsachlichen Kommentaren tust Du Dir selber keinen Gefallen.
Ja - ich weiß (aus jahrzehntelanger Erfahrung mit Studenten) wo die Verständnisprobleme liegen (auch bei Dir !): Viele denken nämlich - nur weil es ein Symbol für eine ideale Stromquelle gibt, dass Stromquellen existieren. Das ist aber nicht der Fall - es gibt nur Spannungsquellen mit einem seriellen Innenwiderstand Ri. Und wenn Ri groß genug ist, dann verhält sich diese Kombination unter bestimmten Randbedingungen FAST wie eine Stromquelle. Und dann kann man - wenn man möchte - die Reihenschaltung aus (idealer und großer) Spannungsquelle und (großem) Ri auch in eine ideale Stromquelle mit Parallelwiderstand umrechnen (umrechnen !) - aber nicht realisieren!! Hast Du es jetzt?
Bedeutet also damit ich immer einen Stromfluss von zb 1A haben möchte, sollte ich ein Innenwiderstand von unendlich haben damit diese 1A vom Lastwiderstand nicht verändert wird? Somit würde der Lastwiderstand keine Rolle spielen, weil ich ein Innenwiderstand von Unendlich habe? Right?