Stereoisomere von 1-Ethyl-3,5-dimethylcyclohexan?

Hallo,

wie kann man alle Stereoisomere von 1-Ethyl-3,5-dimethylcyclohexan zeichnen? Wie muss man da vorgehen?

Für die Beantwortung meiner Frage bedanke ich mich bereits im Voraus.

Answer 1

[indiachinacook]

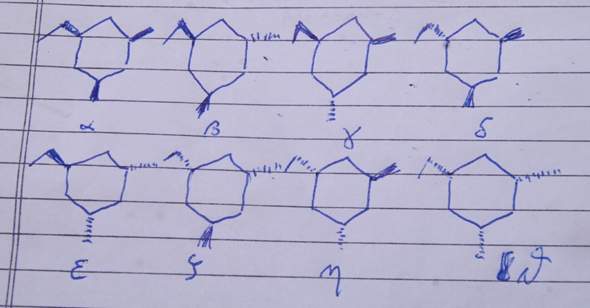
Du tust so, als ob der Ring planar wäre und legst ihn in die Papierebene (er ist nicht in Wirklichkeit nicht planar, aber dazu kommen wir noch). Da Du 3 Substituenten hast, kannst Du die Substituenten räumlich auf 2³=8 Arten anord­nen: Alle ober der Papier­ebene, einen unterhalb (3 Möglichkeiten), zwei unterhalb (auch drei Möglichkeiten) und alle unterhalb. Diese acht Strukturen zeichnest Du Dir auf. Hier kommen sie alle, durchnumeriert von α bis ϑ.

Als nächstes mußt Du Dubletten eliminieren, also die Strukturen, die ein und dasselbe sind. Dazu fragst Du Dich, welche man durch Drehungen des ganzen Moleküls inein­an­der überführen kann, und streichst entsprechend weg.

• α und ϑ sind dasselbe, drehe dazu um eine Achse, die den Mittelpunkt des Sechs­ringes und das C-Atom, an dem die Ethylgruppe hängt, enthält. Dadurch werden die beiden Methylgruppen vertauscht, und alles, was vorher über dem Ring lag, liegt danach darunter. Insgesamt kommt dann jeweils das andere Molekül heraus.
• Ebenso sind β und ζ dasselbe. Die Methylgruppe, die bei β unten und über der Papierebene liegt, kommt nach der Drehung rechts und hinter der Papierebene heraus, genauso wie sie in ζ liegt.
• Durch dieselbe Argumentation sind auch γ und η dasselbe.
• Zuletzt sind auch δ und ε dasselbe

Also haben wir insgesamt vier Stereoisomere gefunden: α, β, γ und δ.

• Dabei bilden β und γ ein Enantiomerenpaar. Das sieht man daran, daß sie durch Spiegelung ineinander übergehen. Spiegelung an der Papierebene führt z.B. β in η über, und wir haben bereits gesehen, daß η und γ dasselbe sind. Man kann aber auch eine Spiegelebene finden, die β direkt in γ überführt; sie muß durch das C-Atom, das die Ethylgruppe trägt, und den Mittelpunkt des Ringes gehen, und auf die Ring- bzw. Papierebene normal stehen.
• Dagegen steht α für sich allein. Du siehst, daß es kein Enantiomer zu irgendetwas sein kann, weil es durch Spiegelung in sich selbst übergeht, also achiral sein muß (nimm wieder dieselbe Spiegelebene wie oben beschrieben).
• Auch δ steht für sich allein, aus demselben Grund.

Wir haben also als Stereoisomere das Enantiomerenpaar β/γ gefunden, und dazu zwei weitere Diastereomere α und δ. Moleküle wie α und δ enthalten zwar asymmetri­sche C-Atome, sind aber nicht chiral; solche Moleküle bezeichnet man auch als meso-Verbindungen, und die gibt es immer dann, wenn Paare oder höhere Tupel von äqui­va­len­­ten asymmetrischen C-Atomen auftreten. In unserem Fall sind die Ringatome, die die Methylgruppen tragen, zueinander äquivalent (ich werde jetzt nicht genau defi­nie­ren, was ich mit äquivalent meine, es sollte eigentlich intuitiv klar sein, daß man die beiden nicht wirklich gut unterscheiden kann).

Zuletzt können wir uns noch optionalerweise dem Problem widmen, daß die Sechs­ringe in Wirklichkeit nicht planar sind, sondern in einer Kronen-Form vorliegen, bei der die Atome abwechselnd unter und über der Papierebene stehen; Du hast also zwei Mög­­lich­keiten, wie Du die Sechsringe falten kannst, und entscheidest Doch dabei für die, die mehr äquatoriale Substituenten hat (bei einem Ringatom, das ober der Pa­pier­ebe­ne zu liegen kommt, ist der Substituent äquatorial, der in der flachen Darstellung unter der Papierebene liegt). Oder alternativ gesagt: Falte die Ringe so, daß die Ato­me, die Substituenten vor der Papierebene tragen, bevorzugt unter die Papierebene zu liegen kommen.

So wie ich die Vögel α–δ aufgeschrieben habe, muß das Atom, das die Ethylgruppe trägt, immer unter die Papierebene. Aber vermutlich wird dieser letzte Schritt von Dir eh nicht erwartet.