Stehen Newton's Formeln wirklich in seinem Buch "Mathematishe Prinzipien der Naturlehre"?
Hallo,
ich wollte kürzlich mal Newton's Buch lesen, habe es dann aber nur überflogen, da Newton kaum mit Gleichungen argumentiert, sondern fast ausschließlich mit Fließtext, was alles sehr langatmig macht.
Mir ist dann eingefallen, dass Infinitessimalrechnung, Limes und Ableitungen u. a. erst von Newton entwickelt wurden, um physikalische Probleme zu lösen und dass diese mathematischen Methoden wahrscheinlich noch nicht existiert haben, als er das Buch schrieb. Allerdings tauchen dann gegen Ende des Buches auch ein paar Integrale auf, was mich dann wieder eher überrascht hat.
Am überraschensten ist aber, dass seine berühmten Formeln, z.B. F = ma (bzw. F = dp/dt), F_G = Gm1m2/r^2, p = mv usw. gar nicht in seinem Buch auftauchen. Zwar argumentiert er mit Worten, dass die Gravitation proportional zu 1/r^2 ist, aber er schreibt keine Formel hin. Im Physikstudium wurde einem immer erzählt Newton habe diesen Formalismus entwickelt, wo man im wesentlichen die Bewegungsgleichung F = ma aufstellt und dann löst. Das tut er in dem Buch aber nicht.
Deshalb frage ich mich jetzt, ob irgendjemand mal gesagt hat, dass diese Gleichungen bzw. dieser Formalismus in Newton's Buch veröffentlicht wurden und das am Ende alle zitiert haben ohne es zu überprüfen und es deswegen heute jeder glaubt, obwohl es gar nicht stimmt?
Bzw. weiß jemand, in welcher Veröffentlichung solche Gesetze, Definitionen und das Lösen von Bewegungsgleichungen dann erstmals in der heute üblichen Notation formuliert wurden?
Danke für alle Antworten und sorry für den langen Text :)
3 Antworten
Ein Formalismus ist nicht dasselbe wie die Symbolsprache, die man zu seiner Darstellung wählt.
Das Sieb des Eratosthenes z.B. ist in Hunderten verschiedener Programmiersprachen und natürlicher Sprachen dargestellt worden. Die Symbole sind verschieden, der Algorithmus ist derselbe
https://rosettacode.org/wiki/Sieve_of_Eratosthenes
Wenn Du das von Leibniz eingeführte Integralzeichen in Newtons 'Principia' gesehen hast, dann war das vielleicht die Genfer Ausgabe:
1739 bis 1742 erschien in Genf eine Ausgabe der 3. Auflage mit ausführlichem Kommentar (beinahe Zeile für Zeile), herausgegeben durch die Franziskaner Thomas Le Seur und François Jacquier (aber auch andere Wissenschaftler arbeiteten daran mit), in der sie auch den moderneren Leibnizkalkül der Infinitesimalrechnung verwendeten.
https://en.wikipedia.org/wiki/Philosophi%C3%A6_Naturalis_Principia_Mathematica
Hier wird über eine ähnliche Frage diskutiert:
https://hsm.stackexchange.com/questions/2362/why-is-calculus-missing-from-newtons-principia
In der Tat sind die heute benutzen Formeln, die die Newtonschen Gesetze beschreiben, nicht so in der Originalschrift zu finden.
So lautet das erste Newtonsche Gesetz im Original:
„Mutationem motus proportionalem esse vi motrici impressae, et fieri secundum lineam rectam qua vis illa imprimitur.“
(„Die Änderung der Bewegung ist der Einwirkung der bewegenden Kraft proportional und geschieht nach der Richtung derjenigen geraden Linie, nach welcher jene Kraft wirkt.“)
Erst Leonhard Euler hat diese wörtliche lateinische Formulierung in die heute übliche Sprache der Mathematik übersetzt und 1750 die Formel aufgestellt:
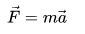
Das ist aber nicht ungewöhnlich. Auch eine der berühmtesten Formeln der Physik:
E = m*c^2 steht so nicht in der Originalschrift von Einstein. Das ist nur die in die heute übliche Schreibweise übersetzte. Im Original lautet diese Erkenntnis:
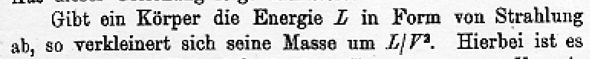

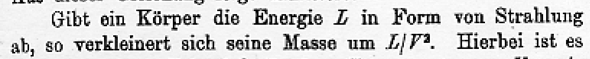
Habe ich auch gedacht...war aber zu faul, mir Eulers Original anzugucken....Der hat womöglich auch andere Formelzeichen verwendet.
ich weiß es nicht was genau in seinem buch steht, aber wenn er zB geschrieben hat dass die gravitationskraft proportional zu den beiden massen und invers proportional zum quadrat des abstandes ist, dann hat er die damit schon hingeschrieben.
Ich vermute aber, daß Euler noch keine Vektorpfeile verwendet hat.