Siedetemperatur von Wasser berechnen?
Hallo,
ich möchte berechnen ab wie viel Grad Wasser unter zb. Den Druck von 64,5 Bar siedet. Dabei möchte ich nicht von Tabellen ablesen, ich möchte es ausschließlich berechnen. Danke für die Hilfe
LG
2 Antworten
Die Gleichung von Clausius-Clapeyron lautet:
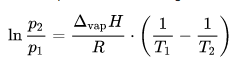
Die müssen wir nach T2 auflösen:
ln(p2/p1) = ∆vapH/(R * T1) - ∆vapH/(R * T2)
∆vapH/(R * T2) = ∆vapH/(R * T1) - ln(p2/p1)
T2 = ∆vapH / R(∆vapH/(R * T1) - ln(p2/p1))
= vapH / (∆vapH/T1 - R*ln(p2/p1))
mit:
∆vapH (Wasser) = 40650 J/mol
R = 8,314 J/molK
T1 = 373,15 K (100 °C)
p1 = 1,0132 bar
p2 = 64,5 bar
ergibt sich:
T2 = 40650 J/mol / (40650 J/mol / 373,15 K - 8,314 J/molK*ln(64,5/1,0132))
= 40650 J/mol / (108,937 J/molK - 34,533 J/molK)
= 40650 J/mol / 74,404 J/molK = 546,34 K = 273,19 °C
Das stimmt alerdings nicht so ganz mit den Tabelllenwerten (= 280,5 °C) überein. Entweder liegt das an Rundungsfehlern oder an einem Rechenfehler meinerseits.
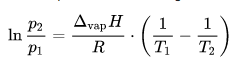
Liegt der Unterschied zum Tabellenwert evtl. daran, daß ∆vapH temperaturabhängig ist?
Ich weiß es leider nicht, wie die Differenz zustande kommt. Ich vermute, dass die Annahme, dass ∆vapH konstant sei, eine Annäherung ist und das weiters die gesamte Gleichung lediglich nur eine Näherungslösung ergibt, die reale Effekte vernachlässigt.
Das macht man mit der Clausius-Clapeyron-Gleichung...
Deine Rechnung stimmt, mit CAS komme ich auf T2 = 546,33574... K. Liegt der Unterschied zum Tabellenwert evtl. daran, daß ∆vapH temperaturabhängig ist?