Seiten im Dreieck aus Seitenhalbierende berechnen?
Ich habe Probleme mit der folgenden Aufgabenstellung:
Von einem Dreieck sind a = 4, sa = 4 und α = 30° bekannt.
Bestimmen Sie die Länge der Seite c.
Zeichnerisch konnte ich die länge schon ungefähr ermitteln, daher weis ich, dass diese irgendwo bei 5,9 liegen muss.
Leider finde ich den rechnerischen Weg nicht.
Vielen danke im vorraus!
2 Antworten
du hättest folgende Zusammenhänge:wobei der bekannte Winkel durch die Seitenhalbierende in zwei Teile geteilt wird, von denen man nur die Summe kennt...
dann hast du also 2 Teildreiecke mit alpha1 einer Seite (sa) und noch einer Seite (a/2)... reicht das für den Kosinussatz? oder was kennt ihr schon?du hast also 4 Unbekannte: b, c und die beiden Teilwinkel... und nur 3 Gleichungen... also noch eine Gleichung: für die Seitenhalbierende gilt:
geht es dann? also WA kommt da auf sehr komplizierte Ausdrücke... und einige Lösungen... allerdings nur zwei mit reellen, positiven Längen... c und b sind 6 und 2 oder umgekehrt... odar?
passt etwas zu deiner Zeichnung...
ja... hast recht... hab grad die Probe gemacht... k. A., was WA sich da ausgedacht hat... lol
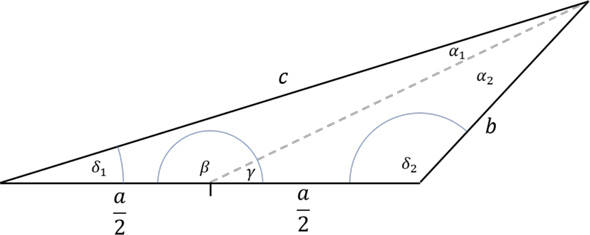
Die Berechnung ist recht aufwändig und ist unter dem link als PDF Datei eingehängt. und unkommentiert dargestellt. Das Einbinden von 9 Bildern scheiterte an den GuteFrage Limitierungen. Das obige Bild ist nach dem Ergebnis b=2,36 und c=5,87 korrekt dargestellt. Du liegst mit Deinen 5,9 LE schon sehr nah an der Wahrheit
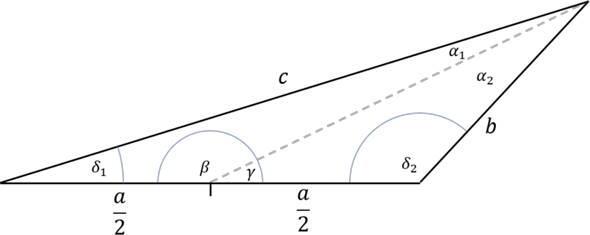
Die Lösung ist laut unterlagen (Mathe Vorkurs Unterlage HAW ) c1 = 5,867 ; c2 = 2,362 (Aufgabe D22)
Ggf. hilft mir der Ansatz! Danke schon einmal!