Schwingkreis - Impedanz und Resonanzfrequenz berechnen
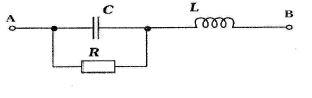
Hallo, ich habe folgenden Schwingkreis gegeben:
Wie berechne ich zu diesem Schwingkreis die Impedanz und Resonanzfrequenz? Bzw. wie ist überhaupt die allgemeine Herangehensweise bei solch ähnlichen Schwingkreisen?
Im Unterricht haben wir bisher immer nur ganz normale Reihen- und Parallelschwingkreise behandelt. Leider habe ich bei dem gegebenen Schwingkreis keine wirkliche Idee, wie man da auf die Impedanz und Resonanzfrequenz kommt.
Über Hilfe wäre ich sehr dankbar!
Gruß!
3 Antworten
ja soweit ich weis ist der wirkwiderstand vom Kondensator sehr hochohmig und deshalb ist der scheinwiderstand von C und R parallel gesehen genauso groß wie der Blindwiderstand von C, da R sogut wie keinen einfluss hat. Daher kann ich ebenfalls sagen, das dies ein reihenschwingkreis ist. So gesehen existiert der parrallele widerstand bei C gar nicht. Daher hast du einen so gut wie reinen Reihenschwingkreis aus C und L.... die Blindwiderstände sind nun äbhängig davon was du für einen frequenz draufgibst. Bei resonanz würde es bedeuten das du einen kurzschluss hast da C und L sich zu 0 subtrahieren, weil du keinen Wirkwiderstand und keinen Blindwiderstand hast. lg winox
Mal ganz einfach...
Für die Resonanzfrequenz ist der ohm'sche Widerstand egal. Der sorgt nur für die Strombegrenzung.
Im Resonanzfall ist XL und XC gleich groß ....
Das ist ein ganz normaler Reihenschwingkeis, also ein "Saugkreis". Der ohmsche Widerstand soll nur verwirren, er hat keinen direkten Einfluss auf die Frequenz. Nun ja, er verringert als Stromteiler eben den Blindwiderstand der Kapazität.
Also nehme ich da die ganz normale Formel Z = R + j(wL - 1/wC) und f = 1/2pi*wurzel(LC) ?
Nimm die Reihenschwingkreis-Formel wie du sie kennst und du bist auf der sicheren Seite.
Das wäre doch nur der Fall bei einem reinen Serienschwingkreis, oder nicht? Bei diesem wäre der Widerstand durch seine rein Strombegrenzende Wirkung (die sich ja ohne Vermaschung auf ALLE Teile erstreckt) für die Resonanzfrequenz unwichtig, da nur eine Art "Ergänzung" der Realverluste.
Ich hätte aber gedacht, daß sich durch den parallelen ohmschen Widerstand die Kombination verhält wie ein stark verlustbehafteter Kondensator, der sich dadurch langsamer auf seine Soll-Ladung auflädt, und einen Teil des Stromes in Phase mit der Quellspannung, als Gesamtelement zwar mehr Strom durchläßt, da Schein- und Wirkwiderstand verringert, aber eben für die Aufladung des Kondensators (wie erhöhte Kapazität) in Betracht auf f-null dämpfend wirkt, und so die Resonanzfrequenz erniedrigt?
Oder: Wie durcheinander bin ich? ^^