Schiefer Wurf mit Anfangshöhe ohne Anfangsgeschwindigkeit berechnen?

Hallo zusammen habe eine Frage zum Thema Physik,

ein Golfball (m=0,07Kg) schießt eine Rampe hoch und fliegt am ende der Rampe Parabelförmig mit einer Anfangshöhe von 0,6m und einen Winkel der Rampe von 13,5° hoch, und soll das 3 Meter entfernte Loch direkt treffen.

Wie hoch ist v_0 bzw. die Anfangsgeschwindigkeit?

PS: Die Masse ist unwichtig für die Aufgabe

Vielen Dank im voraus und bleibt gesund!

Answer 1

[Bellefraise]

Na dann mal los . . . wie weit bist Du, bzw. wo gehts nicht weiter?

Im schrägen Wurf haben wir die Geschwindigkeiten

vx = v0 * cos(a)

vy = v0 * sin(a)

die Wege

sx = v0 * cos(a) t

sy = v0 * sin(a) * t - 1/2 * g * t^2 (Erdbeschl. zieht nach unten)

Wenn man die Flugkurve über eine Parabel beschreibt, erhält man

Comments

[420Bud]

und wo genau kommt die Höhe h_0=0,6m ins spiel?

[Bellefraise]

@420Bud

das ist in meinen Gleichungen sy

[420Bud]

@Bellefraise

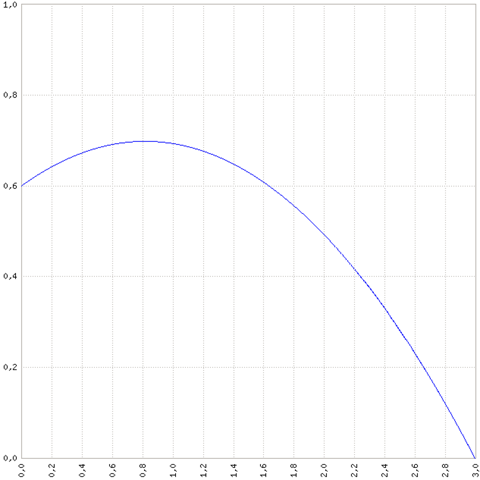
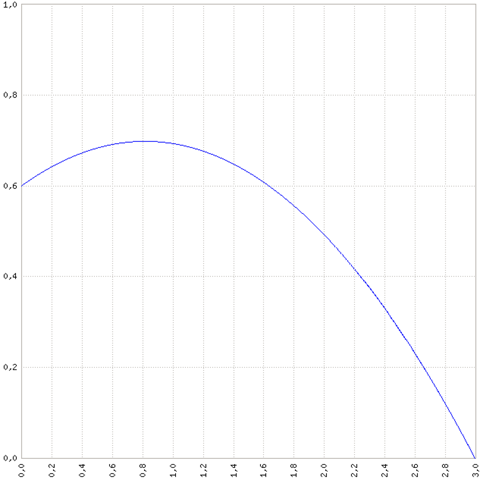
wenn ich die Geschwindigkeit Gleichungen auf v_0 umstelle und gleichsetze hab ich ja immer noch 2 fehlende unbekannte v_x/y auf jeweils einer Seite der Gleichung

[Bellefraise]

@420Bud

versteh ich nicht . . wir haben

sx = v0 * cos(a) * t

sy = v0 * sin(a) * t - 1/2 * g * t^2

Daraus:

v0=sx/(cos(a)*t)

v0=(sy-1/2*g*t^2)/(sin(a)*t

gleichsetzen . . . dann ist nur noch t unbekannt . . . nach t auflösen

[420Bud]

@Bellefraise

ja aber da setzt voraus das wir die Geschwindigkeit v_0 wissen.

Tun wir ja nicht die ist ja gesucht.

[Bellefraise]

@420Bud

Gleichsetzen bedeutet: v0=v0 . . damit fällt v0 weg... also hier:

sx/(cos(a)*t) = (sy-1/2*g*t^2)/(sin(a)*t)

[420Bud]

Okay doch noch eine frage xd, wenn ich die Geschwindigkeiten Gleichung auf v_0 umstelle hab ich ja trotzdem noch unbekannte v_x/v_y und v_0, wie soll ich das denn auflösen?

[420Bud]

Das verdeutlicht es natürlich ungemein, die nette Nutzerin fjf100 hat mir oben schon die Formel umgeschriebene gezeigt.

mit den Ausgangsformeln und den Rechenweg von ihnen ist es aber natürlich direkt plausibler.

hab die Lösung jetzt auch endlich rausbekommen vielen Dank auch dir nochmal für die Unterstützung und deine Zeit.

Bleib gesund.

LG

[Bellefraise]

hier noch der Rechenweg:

die obigen Gleichungen (2. Satz) nach v0 umstellen, beide v0 gleichsetzen,darsua t bestimmen, mit t in eine der Weggleichungen gehen und v0 berechnen. Probe machen, ob mit den berechneten Werten für t und v0 sx und sy berechnet werden können

Answer 2

[Bellefraise]

tipp... lege den koord ursprung in (0/0,6)

Comments

[420Bud]

Hallo und danke für die Antwort, mit dem verschieben des Koordinatenursprungs hab ich schon probiert aber wie bereits oben geschildert komm ich nicht auf die richtige lösen.

Es geht auch eher ums die Rechnung bzw. welche Formel ich benutzen soll

[Bellefraise]

@420Bud

moin.... ist das gelöst oder brauchst du noch infos?

[420Bud]

@Bellefraise

Moin, ich bin ehrlich gesagt am verzweifeln, falls du noch paar Infos und Tipps hättest wäre es super :-)

[Bellefraise]

@420Bud

kriegen wir hin . . . erst mal bitte: wo liegt das Loch.... auf bodenebene oder auf höhe des Ablösepunktes ...

[420Bud]

@Bellefraise

Also, das Loch (Punkt B) liegt 3m vom Punkt A (Anfangsort), der Ball rollt einer Rampe hinauf und verlässt die Rampe in der höhe von 0,6m über dem Punkt A.

D.h. der Ball verlässt an am Punkt A in einer höhe von h_0=0,6m die Rampe.

Geg. ist also die Anfangshöhe h_0=0,6m, die Wurfweite x_w=3m und der Winkel den ich ausgerechnet habe von α=13,5°.

Gesucht ist v_0 , also die Geschwindigkeit mit der der Ball die Rampe verlassen muss um genau auf Punkt B zu landen

[420Bud]

@420Bud

Den Winkel habe ich übrigens mit dem arctan ausgerechnet, geg. war die Länge der Rampe in x-Richtung 2,5m(a) und natürlich die Höhe 0,6m(b)

Also, arctan(b/a)=13,5°

[420Bud]

@420Bud

Das loch liegt also 0,6m unter der abwurfstelle*

[Bellefraise]

@420Bud

danke... ich melde mich ... backe gerade ....

[420Bud]

@Bellefraise

Das wäre nett danke im voraus!

Answer 3

[fjf100]

siehe Physik-Formelbuch,was man privat in jedem Buchladen bekommt.

Kapitel,Kinematik,schräger Wurf,

Bahngleichung des schrägen Wurfs

y=h(x)=-g/(2*Vo²*cos²(a))*x²+tan(a)*x

bei x=0 ist h(0)=0,6 m also

h(x)=-g/(2*Vo²*cos²(a))*x²+tan(a)*x+0,6 m

bei x=3 m ist h(3)=0

0=...

nun nach Vo umstellen

g/(2*Vo²*cos²(a))*x²=tan(a)*x+0,6

Vo²=[g/(2*cos²(a))*x²]/[tan(a)+0,6]

Betrag Vo=Wurzel(......)

(a)=13,5° x=3 m

g=9,81 m/s² ist die Erdbeschleinigung

Im Physik-Formelbuch findest du auch der Herleitung und eine Zeichnung

Woher ich das weiß: Studium / Ausbildung – hab Maschinenbau an einer Fachhochschule studiert

Comments

[420Bud]

Hey und danke das du dir die Zeit genommen hast mir zu antworten, ich habe ein Physikbuch zuhause Physik für Bachelors Johannes Reybach.

Das Buch sagt aber nicht viel zu dem Thema und schon Garnichts zum Schiefen Wurf mit einer Anfangshöhe.

Mit deiner Rechnung komme ich auf ~0,83 m/s was mir ein wenig zu gering erscheint.

Ich bin schon seid mehreren Stunden an dieser Aufgabe und Onlinerechner sagen mir das Ergebnis ist ~5,95m/s aber ich benötige eine Rechnung

Ich habe schon einige Rechnungen Probiert und habe auch schon alles umgestellt was ging aber auf das Ergebnis komm ich nicht.

[fjf100]

@420Bud

Vo=5,95 m/s stimmt

Betrag Vo=[g*x²/(2*cos²(a))]/(tan(a)*x+0,6) mit x= 3 m und (a)=13,5°

Vo=[9,81 m/s²*(3 m)²/(2*cos²(13,5°))/(tan(13,5°*3 m+0,6 m)=5,9468..m/s

Vo=5,95 m/s.

[420Bud]

@fjf100

vielen Dank nochmal, aber wie gesagt kommt das Ergebnis dabei nicht raus, ich habe es genau mit dieser schreibweis nochmal durchgerechnet, auch über die Seite WolframAlpha (falls es ihnen was sagt) mir wird das Ergebnis 470,197 angezeigt.

Ich habe auf alles geachtet (korrekte Schreibweise Klammersetzung etc.)

[fjf100]

@420Bud

Man,bist du ein schwerer Fall !

g*x²/2=9,81/2*(3 m)²=44,145

44,145/(cos(13,5°))²=46,689..

tan(13,5°)*3 m+0,6m=1,3202..

Vo=Wurzel(46,689/1,3202)=5,9467..m/s=5,95 m/s

Überprüfung

Bewegung in y-Richtung

1) a=-g

2) Vy(t)=-g*t+Vy → sin(a)=Vy/Vo → Vy=sin(13,5°)*5,95 m/s=1,388..m/s

3) S(t)=h(t)=-1/2*g*t²+Vy*t+h → h=0,6 m

Flugzeit h(t)=0=-1/2*9,81 m/s²*t²+1,388 m/s*t+0,6 m ist eine Parabel der Form

f(x)=a2*x²+a1*x+ao

Nullstellen mit meinem Graphikrechner (GTR,Casio)

t1=-0,2357.. s

t2=0,5189 s

also Flugzeit t=0,5189 s (Sekunden)

Bewegung in x-Achtung

sx=vx*t=cos(a)*Vo*t=cos(13,5°)*5,95 m/s*0,5189 s=3,00 m also richtig

also Abschußgeschwindigkeit Vo=5,95 m/s unter einen Abschußwinkel von (a)=13,5°.

[420Bud]

@fjf100

Ja das bekomm ich oft zuhören, nochmals danke für die Formel, habs jetzt ausprobiert komme aufs gleiche Ergebnis

Answer 4

[fjf100]

Infos,vergrößern und/oder herunterladen

Woher ich das weiß: Studium / Ausbildung – hab Maschinenbau an einer Fachhochschule studiert