Schafft es jemand dieses Mathematik Rätsel zu lösen?
Die beiden "a" Seiten sind gleich langEins steht für 1cm, Zwei für 2cm usw.
Brauche selber Hilfe also wenn möglich mit Rechenvorgang
Danke!

4 Antworten
Hat die gerade mit 1 cm 45°?
Hat die gerade mit 1 cm 45°?
Kann nicht sein, denn dann wäre es die Winkelhalbierende, und dann müssten die beiden andere Strecken gleich lang sein.
Wir haben das Rätsel von unserem Mathelehrer bekommen also weis ich selber nicht genau ob es 45° sind.
Ist es 3.623cm?
Also mit der Annahme, dass das 45° sind, komme ich auf 3.623cm.
45° kann nicht sein, denn dann wäre es die Winkelhalbierende, und dann müssten die beiden andere Strecken gleich lang sein.
Das Gleichungssystem löst man am besten durch ein Additions- bzw.Subtraktionsverfahren der beiden letzten (ausmultiplizierten) Gleichungen und erhält dann jeweils einen Ausdruck für y-x und y+x. Durch abermalige Addition dieser beiden Gleichungen isoliert man x und y. Das kann man dann in x^2+y^2=1 einsetzen und erhält ein quartisches Polynom in a mit ausschließlich geraden Exponenten. Daher können wir die p-q-Formel benutzen und erhalten u.A. unsere gesuchte Lösung:
a=sqrt( (13+sqrt(23))/2) = 2,9829.....
Das erscheint auch durchaus plausibel, da a nicht größer als 3 sein kann, weil sich sonst der Kreis mit Radius 1 und Radius 2 nicht schneiden würden.
VG GregoryGnom
Ich beziehe mich auf die drei Gleichungen, die schon korrekt von https://www.gutefrage.net/frage/schafft-es-jemand-dieses-mathematik-raetsel-zu-loesen#answer-222947701 erstellt worden sind.
Unabhängig von der Ausrichtung der gerade mit Länge 1 muss es sich so lösen lassen. Bin aber noch nicht draufgekommen wie das gleichungssystem zu lösen ist. vielleicht denk ich auch zu kompliziert.
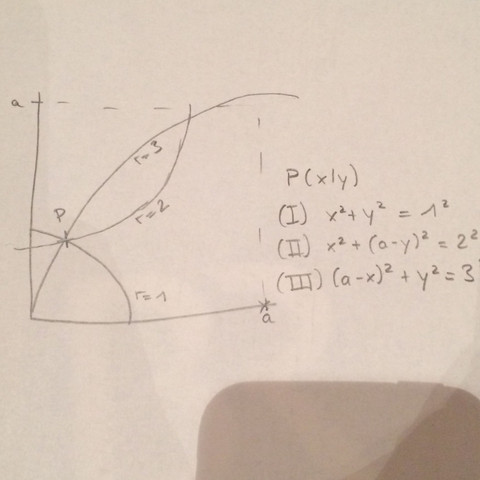
Stell dir das Quadrat als Koordinatensystem vor.
Wenn die gerade mit Länge 1 die Winkelhalbierende ist, fünft sie am Punkt 0|0 an und endet am Punkt Wurzel(1/2)|wurzel(1/2)
Die gerade mit Länge 2 fängt am Punkt (0|a) an und geht zum Punkt Wurzel(1/2)|wurzel(1/2).
Dann hast du die Gleichung:
2^2 = 0,5 (x-Unterschied) + (a-wurzel(1/2)) ^2
Also a^2 - a*wurzel(1/2) + 0,5 = 3,5
Dann hast du:
a^2 - a*wurzel(1/2) -3 =0
Das dann in die mitternachtsformel und du hast es.
Du kannst es natürlich auch mit einem gleichungssystem machen wenn du a für die gerade mit Länge drei noch ausrechnest. Aber ein Wert aus der mitternachtsformel lässt sich eh ausschließen weil er negativ ist.