Quadratische Funktionen Ist meine Rechnung richtig?
Hallo!
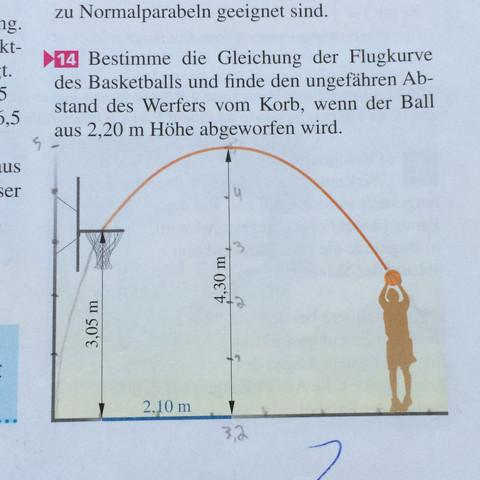
Für meinen Nachhilfeschület wollte ich folgende Aufgabe lösen, aber da ich die quadratischen Funktionen vor 2 Jahren hatte, bin ich mir nicht mehr sicher, ob meine Lösung auch richtig ist.
Ich bin am Ende zu dem Entschluss gekommen, dass der Werfer ca .4,2 meter entfernt ist.
Meine Rechnung und die Aufgabe findet ihr im Anhang.
Vielen Dank im Voraus!

2 Antworten
Also ich komme ziemlich genau auf 4,8 und das ziemlich bezieht sich dabei auf Rundungsfehler bzw. abgeschnittene dezimalstellen. Ich kann deine Rechnung auch nicht ganz nachvollziehen, da diese Aufgabe auch sehr schnell gelöst werden kann. Ich würde sowieso niemals empfehlen in Mathrbücher Angaben zu schreiben, da diese zu 90% nie Maßstabsgetreu sind. Daher bringt es nichts mit dem Lineal zu gucken "okay hier müsste laut dem Bild, der und der Wert sein".
Aber mal zur Rechnung.
Was wissen wir?
Dein Koordinatenkreuz kannst du so legen, dass du den Punkt P1 = (0 | 3,05 ) erhältst. Das hast du anscheinend auch noch gemacht.
Den zweiten Punkt kann dann sehr leicht ablesen. Es ist der Scheitelpunkt
S = (2,1 | 4,3)
Aus der Scheitelpunktform wissen wir daher sofort das x_s und y_s
D.h.
f(x) = a(x-2,1)² + 4,3
und aus P1 ebenfalls in SPF
3,05 = a(0-2,1)² + 4,3 = 4,41a + 4,3 Eine Gleichung, eine Variable.
Da die Parable nach unten geöffnet ist, wissen wir das a negativ sein muss:
Stellst du die Gleichung nach a um erhälsts du:
a= -0,283... also das VZ stimmt schon mal.
Jetzt hast du deine komplette Gl. f(x) = -0,283(x-2,1)² + 4,3
Der Ball befindet sich auf der Parabel mit der "Höhe" 2,2
Also
2,2 = -0,283(x-2,1)² + 4,3
Löst du das nach x auf erhälst du
x= 4,8....
Entsprechend befindet sich dein Werfer 4,8 Meter vom Korb weg.
Und noch ein EDIT: Du hast das hier gemacht (siehe Bild) Die Nullstellen zu bestimmen ist falsch, da sich dein Werfer selbst nicht auf dem Graph befindet, sprich er selbst ist x, nicht f(x) !!! Du hast mit den Nullstellen die rotmarkierten Kreise bestimmt, du willst aber den braunen haben.
Zudem:
Die Nullstellen dann zu addieren macht interpretativ absolut keinen Sinn!
