Normalkraft in der schiefen ebene?
Hat man einen flachen Untergrund so ist die normalkraft die der Boden auf ein Objekt auswirkt genau so groß wie die gravitationskraft. Hat man nun eine schiefe Ebene so wird die normalkraft immer kleiner mit steigendem Winkel weil die hangabtriebskraft ja größer wird, aber warum wird die normalkraft kleiner das Objekt drückt doch nach wie vor auf den Untergrund ?
5 Antworten
Wie schon bei andern Fragen erwähnt, halte ich nichts von einer Gravitationskraft, die "sich" plötzlich ganz eigenwillig in zwei Komponenten "aufteilt". Das mag als simple Deutung des Hangabtriebs in der Grundschule genügen, trotzdem muss man dafür ja die Vektoraddition verstehen.
Durch Vektoraddition dieser zwei oder drei Kräfte (wie in der Skizze von Halbrecht) erhält man aber entweder nur wieder die Gravitationskraft, oder gar das Doppelte davon! Das ist also physikalisch gesehen Mumpitz, weil sich das Objekt ja nicht durch die Unterlage hindurch beschleunigen kann! Weder durch eine schiefe noch eine horizontale.
- Die Gravitationskraft zeigt unveränderlich und immer schön senkrecht nach unten
- Die Reaktionskraft der Unterlage (nach Newton!) zeigt senkrecht zur Unterlage nach oben, sie heisst Normalkraft. Und sie ändert halt ihre Lage und Stärke, wenn die Unterlage schief wird.
- Nun entscheidet man (ebenfalls nach Newton!) mit Hilfe der Vektoraddition und aufgrund der Aufgabenstellung, was das Objekt machen soll:
- Falls das Objekt ruht oder sich konstant aufwärts oder abwärts bewegt, gibt es eine dritte Kraft, die zusammen mit Fg und FN vektoriell addiert null ergeben muss.
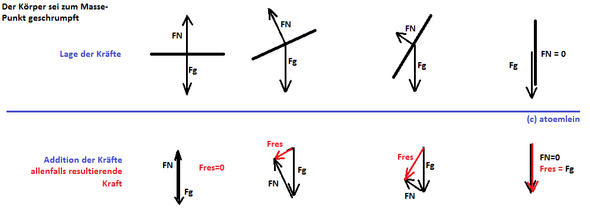
- Falls das Objekt beschleunigt abwärts rutscht, muss durch Addition von Fg und FN eine resultierende Kraft entstehen. Und diese resultierende Kraft kann man Hangabtriebskraft nennen. Hier die Beispiele mit den Hangneigungen von 0 bis 90 Grad:
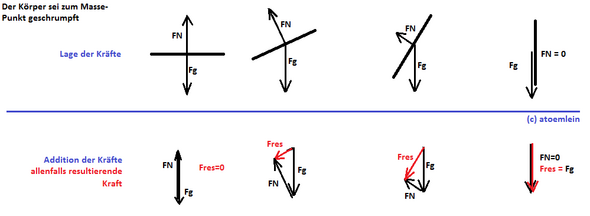
Im Ruhefall würde der rote Pfeil in die Gegenrichtung zeigen und wäre die dritte Kraft, mit welcher die Vektoraddition im Kräftedreieck null ergibt.
"Gewicht" ist ein verwirrender Begriff.
Nein, das würde ich nicht.
Ich verstehe nicht, warum du noch nach weiteren Erklärungen für die Abnahme von FN suchst; mit beiden Methoden, die als Antworten kamen, hast du sowohl eine geometrische wie eine physikalische Deutung. In den Grenzfällen der senkrechten oder waagrechten Unterlage dürfte es sogar ohne Physik und GEometrie einleuchten.
Noch zum "Gewicht":
Im Volksmund wird "Gewicht" leider oft gleichgesetzt mit Masse. Die Masse eines Körper ist ja in jedem Fall ortsunabhängig, egal ob das Objekt auf der Erde oder dem Mond, oder im Waser oder im Vakuum, oder auf schiefer oder horizontaler Unterlage ist.
In der Physik kann "Gewicht" höchstens für die Gewichtskraft verwendet werden, die sich immer aus Masse mal Schwerebeschleunigung (Ortsfaktor) ergibt. Sie ist also nicht konstant, wenn sich der Ort ändert.
Waagen messen die Masse, in dem sie die Gewichtskraft messen und diese mit der Gravitationsbeschleunigung auf der Erde verrechnen. Eine Personenwaage zum Beispiel würde auf dem Mond also eine falsche "Masse" vorgaukeln.
Ob man nun so argumentieren kann, und was es bringt, ist Ansichtssache. Für mich ist die Gewichtskraft die Gravitationskraft, sie bleibt am Ort konstant und kann nicht anders als senkrecht nach unten zeigen.
Wenn man sich natürlich auch andere Modelle zurechtlegen. Verboten ist das nicht, nur vielleicht nicht immer konsequenz und nicht auf andere Probleme übertragbar.
Von mir aus kann man sagen, dass die schiefe Ebene einen Teil der Gewichtskraft parallel entlang der schiefen Ebene "umleitet", ableitet, so wie Regen an einem Dach. Damit ist aber noch nicht gesagt, dass der restliche Anteil eine Normalkraft, also senkrecht zur Unterlage, sein muss, und wie gross sie ist.
Das stimmt aber ich meine selbst wenn man eine schiefe Ebene hat und der Betrag der normalkraft egal bei welchem Winkel gleich dem Betrag der Gravitationskraft wäre. Dann könnte man doch trotzdem noch eine vektoraddition durchführen oder nicht?
Ja.
Ich glaube, ein anderer Antworter hat bei einer andern Frage von dir gesagt, man könne sicher dann die Kräfte als Vektoren addieren, wenn sie den gleichen Angriffspunkt haben. Ich denke, das stimmt; noch genauer: Wenn sich ihre Wirkungslinien in einem Punkt schneiden. Dies ist sicher dann der Fall, wenn man den fraglichen Körper als Masse-Punkt auffasst.
Beim ersten Teil der Nachfrage bin ich nicht sicher, was zu meinst:
"...selbst wenn man eine schiefe Ebene hat und der Betrag der normalkraft egal bei welchem Winkel gleich dem Betrag der Gravitationskraft wäre..."
- Betrag der Normalkraft ist NUR bei horizontaler Unterlage gleich Gravitationskraft
- Auch schiefe und gleich grosse Kräfte kann man vktoriell addieren
Ja das stimmt eventuell habe ich es irgendwo überlesen aber gibt es eine physikalische Erklärung dafür warum die normalkraft kleiner wird in der Ebene ? Das mit dem Extremfall 90 grad macht natürlich Sinn aber wir versuchen ja mit den echt wirkenden Kräften (Gravitation und normalkraft) die hangabtriebskraft zu erklären dann kann man doch nicht im umkerhschluss sagen, da es eine hangabtriebskraft gibt muss Fn kleiner werden
Doch, das kann man, falls man alle andern Ursachen ausschliessen kann, welche sonst noch das Objekt nach unten ziehen könnten (z.B. noch ein Magnet). Dies eben wegen der Vektoraddition: Normalkraft und Hangabtriebskraft haben allein die Gravitationskraft als Ursache, sie können also (vektoriell addiert) nicht grösser sein als die Gravitationskraft.
Das stimmt aber vektoriell addiert da die normalkraft nach oben zeigt und die hangabtriebskraft schief nach unten, so würde eine nach oben gerichtete Gravitationskraft herauskommen
Bzw in deiner Zeichnung passt es ja schon aber müssten nicht beide Kräfte also Fg und Fn in gleichem angriffsöunkt addiert werden und Fhang zu erhalten? Wenn man das nämlich so macht müsste man die andern Kräfte ja subtrahieren um Fg zu erhalten und nicht addieren
Also nochmal:
- Vektoraddition bedeutet: Alle Pfeile im gleichen Angriffspunkt addiert man richtungsgetreu, und zwar immer so: An der Pfeilspitze des ersten hängt man den Pfeilanfang des nächsten Vektors an.
- Die Subtraktion eines Vektors ist die Addition seines entgegengesetzt zeigenden Vektors (gleiche Länge, gleiche Richtung).
- Die Reihenfolge ist egal. Wenn man fertig ist, erhält man
- entweder eine resultierende Kraft, die vom Anfang des ersten zur Spitze des letzten Vektors zeigt,
- oder eben eine geschlossene Figur, wo der Pfeil des letzten Vektors mit dem Anfang des ersten zusammenfällt. Dann gibt es keine resultierende Kraft, das Objekt ändert seine Geschwindigkeit oder seine Richtung nicht.
Ja, deine Rechnung stimmt (FHA = Hangabtriebskraft):
- Ich zeichnete Fg + FN = FHA (= Fres), daraus folgt die algebraische Subtraktion:
- Fg = FHA - FN , und das zeigt eben den Denkfehler des andern Ansatzes, der FHA + FN = Fg behauptet (wobei FN hier nach unten zeigen muss). Und diese Addition gibt als "Resultierende" eine senkrechte Kraft, aber das Objekt kann sich ja gar nicht so verhalten.
Was mich nur ein wenig irritiert hat in deiner Zeichnung hast du ja Fg entlang seiner wirkungslinie nach oben verschoben um sie mit Fn zu addieren. In einem andern Beitrag aber hast du Fg an die Spitze von Fn gehangen. Kann man das einfach so machen weil dann verschiebst du ja Fg nicht entlang seiner wirkungslinie sondern eine wenig versetzt nach links oben
Denn die resultierende Kraft also Fha müsste doch auch denselben Angriffspunkt haben wir Fg und Fn und das hat sie ja in der Zeichnung oben nicht
Genau, Fha hat den gleichen Angriffspunkt wie Fg und Fn.
In der Zeichung ist aber Fha noch nicht gezeichnet.
Sie müsste in den Lageplänen (obere Zeile) eingezeichnet werden.
Im Additionsplan gibt es keine Angriffspunkte mehr, weil hier ja die Vektoraddition durchgeführt wird, wofür die Vektoren verschoben werden müssen.
Das ist richtig aber wann darf man sie verschieben? Du sagtest ja entlang ihrer wirkungslinie aber hängt man Fg oben an Fn dran dann dann nimmt man Fg aus seiner wirkungslinie raus.
Oder darf man allgemein Kräfte addieren deren wirkungslinie einen Schnittpunkt haben’s
Also nochmals:
- Für eine Vektoraddition eignen sich Kräfte, die im Lageplan (also dort wo sie effektiv sind) am gleichen Angriffspunkt angreifen (meist beim Masse-Punkt), oder deren Wirkungslinien sich in einem Punkt schneiden (ob Fha nun in der Mitte unter dem Körper oder an der unteren Ecke angreift, ist völlig egal).
- Zur Addition darf man die Vektoren an beliebige Orte verschieben, da spielen Angriffspunkte und Wirkungslinien keine Rolle mehr. Nur Richtung und Länge muss man beachten.
- Und ja, es kann ein Drehmoment entstehen bei unterschiedlichen Angriffspunkten an einem realen Körper.
Bzw wenn wir von starren Körpern sprechen ist das ja was anderes aber kann bei starren Körpern nicht auch ein Drehmoment enstehsten ?
Ok aber dürfte ein Drehmoment nicht nur dann entstehen wenn die Kräfte parallel liegen? Weil in jedem anderen Fall haben die wirkungslinien ja einen Schnittpunkt
Nein, für ein Drehmoment braucht es "nur" unterschiedliche Angriffspunkte und unterschiedliche Wirkungslinien. Das mit den Wirkungslinien war auf die Vektoraddittion bezogen.
Im Allgemeinen Fall (zwei beliebig gerichtete Kräfte an verschiedenen Angriffspunkten eines Körpers) entsteht beides:
Ein Drehmoment und eine resultierende Kraft, welche das Ding "vorwärts" beschleunigt.
Aber wieso soll man dann durch verschieben mit den wirkunsglinien und vektoraddition eine resultierende Kraft ermitteln, wenn auch gleichzeitig Win Drehmoment entsteht?
Aber man kann also Kräfte (bei starren körpern) verschieben und wenn die wirkunsglinien einen Schnittpunkt haben kann man damit die Fres ermitteln?
Nicht ganz, ich hab das vielleicht in mehreren Antworten nicht immer gleich genau geschrieben.
- Fres kann man immer ermitteln
- Kräfte kann man entlang ihrer Wirkungslinie beliebig verschieben, ohne dass sich ihre Wirkung ändert
- Wenn die Kräfte nicht eh am gleichen Punkt angreifen, dann greift Fres am Schnittpunkt ihrer Wirkungslinien angreift dann
- Ein Drehmoment entsteht aber nicht immer. Nur bei verschiedenen Angriffspunkten und wenn z.B. zwei Kräfte nicht gerade zwei gegensätzliche Drehmomente erzeugen.
Normalkraft bedeutet: Diese Kraft drückt "senkrecht" auf die Fläche.
Auf der Erdoberfläche ist Fg=Normalkraft=Fn
Bei der "schiefen Ebene" ergibt die "Vektoraddition" von Fh (Hangabtriebskraft) und Fn (Normalkraft,wirkt senkrecht) die Gewichtsgraft Fg.
Fg wirkt immer auf den Erdmittelpunkt zu.Sie steht senkrecht auf der Erdoberfläche.
Das Objekt drückt bei der schiefen Ebene mit der "Normalkraft" (Fn) senkrecht auf die Oberfläche und nicht mit Fg.
Nach Newton müsste sich also das Objekt dann senkrecht durch die Unterlage hindurch beschleunigen...
Eine Kraft ist immer das Produkt aus Masse m mal Beschleunigung a
1) Fall : Man sieht,wie die Masse m schneller oder langsamer (Bremsvorgang) wird
2) man sieht nix,aber die Beschleunigung ist aber wirksam.
Beispiel: Gewichtskraft Fg=m*g mit a=g=9,81 m/s^2
Man steht auf der Erde und nix bewegt sich,aber g=9,81 m/s^2 wirkt aber auf die Masse m des Körpers.
Genau so wirkt dann die Normalkraft Fn, steht senkrecht auf der schiefen Ebene.
https://www.grund-wissen.de/physik/mechanik/kraftwandler-und-getriebe/schiefe-ebene.html
Auf der Ebene ist die NK gleich der Gewichtskraft (GK) , weil es ja keinen Hang gibt . Sobald ein Hang ins Spiel kommt , wird die GK in zwei Komponenten aufgeteilt : HK und NK. Da aber die GK die Summe von HK und NK sein muß , bewirkt das Auftauchen von HK ein Absinken der NK.
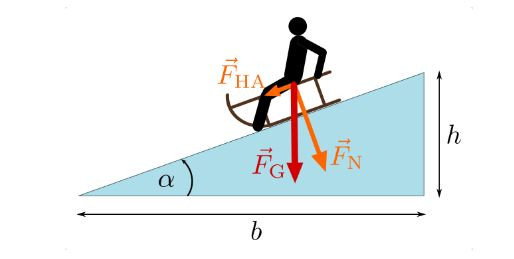
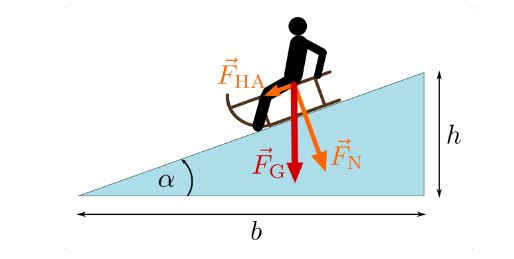
Nicht mehr die ganze Kraft wirkt auf den Boden, sondern wird eben ergänzt durch die Hangabtriebskraft.
Du kannst dir das ja auch gut vorstellen. Wenn du den Winkel des Bodens erhöhst, dann wird dein Objekt immer weniger am Boden haften bleiben. Wenn du dann 90° erreicht hast, dann wirkt deine Normalkraft gar nicht mehr, sondern dein Objekt fällt nur noch runter.
Das Objekt drück eben nicht direkt auf den Untergrund sondern weiterhin senkrecht nach unten.
Die Kraft wird dann aufgeteilt in Normallkraft, die auf den untergrund drückt, und Hangabtriebskraft, die Parallel zum Untergrund verläuft...
Ach so, und nach Newton müsste sich dann das Objekt also senkrecht (Vektoraddition dieser Kräfte) durch die Unterlage hindurch beschleunigen...
Die Objekte werden gegen die Unterlage beschleunigt und daran quasi festgedrückt...
Diese Betrachtung reicht ja meist nicht. Wie soll man darstellen, dass der Körper rutscht?
Es ist bei der hier mehrheitlich vertretenen Betrachtungsmethode nicht klar, welche der drei Kräfte (Fg, FN, FHA) effektiv wirken und welche zur Beschleunigung bzw. zum Verharren im aktuellen Zustand des Körper führen.
Die Hangabtriebskraft ist die Kraft, die en Körper zum rutschen bringt.
Dagegen wirkt die Reibungskraft, die sich aus der Normalkraft mittels des Haftreibungskoeffizienten berechnet...
Wie du vielleicht meiner Antwort entnehmen konntest, ist mir das schon klar!
Aber diese abstruse Aufteilung der Gravitationskraft bringt einen früher oder später in Argumentationsnotstand. Ich kann mir nicht erklären, wie solches in viele Schulen und gar Unis Einzug halten konnte.
Klar...
Die Gegenkraft zur gewichtskraft wird aufgespalten und nicht die Gewichtskraft selbst...
Die Gewichtskraft kann ja schließlich nicht verschwinden...
Und schon bist du im Salat drin.
Welches ist denn auf der schiefen Ebene deine Gegenkraft zur Gewichtskraft?
Das ist ja eben die nach oben zeigende Normalkraft, und die braucht man nicht aufzuspalten.
Und in was spaltest du die auf?
Die Normalkraft ist nur dann die Gegenkraft zur Gewichtskraft, wenn die Fläche eben ist.
Bei einer Schiefen Fläche würde die Gegenkraft allerdings auch senkrecht nach oben wirken.
Sie stimmt aber nicht mitr der Normalkraft überein, da die Normalkraft vond er Fläche weg wirkt und somit nur einen Bruchteil der Gegenkraft entspricht.
(So würde ich das sehen... Dann müsste man das aber weiter denken und müsste sich fragen, ob die Hangabtriebskraft jetzt ein Teil der Gewichtskraft oder ein Teil der Gegenkraft zur Gewichtskraft ist.)
Aber kann man nicht irgendwie argumentieren dass das Gewicht des Objekts was aufliegt kleiner wird und Fn dadurch kleiner wird ?