Mathematik Baumdiagramm?

Könnte jemand mir bei dieser Aufgabe helfen und mir zeigen, wie man das in einem Baumdiagramm rein zeichnet weil ich komme bei diesen Aufgaben nicht gut klar wenn ich ein Baumdiagramm zeichnen muss, wie ich den Anfang davon starten soll das wäre sehr lieb

Answer 1

[mihisu]

Jeder der drei Mittelstürmer schießt einmal. Dementsprechend kann man das Baumdiagramm in 3 Schichten unterteilen... Eine Schicht für A, eine Schicht für B eine Schicht für C.

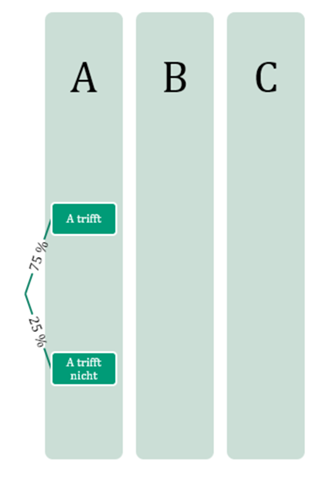
Nun beginnt man links von einem Startpunkt ausgehend. Man hat nun die erste Schicht für A vor sich... Es gibt zwei Möglichkeiten... „A trifft“ (mit Wahrscheinlichkeit 75 %) oder „A trifft nicht“ (mit entsprechender Gegenwahrscheinlichkeit 25 %).

Bei solchen Verzweigungen schreibt man die Wahrscheinlichkeit, mit der man (ausgehend davon, dass man bereits am entsprechenden Punkt vor der Verzweigung ist) den entsprechenden Zweig entlang geht an den Zweig ran. In diesem Fall hat man eine Wahrscheinlichkeit von 75 %, dass A trifft, sodass man die entsprechende Wahrscheinlichkeit an den entsprechenden Zweig schreibt.

Wenn man bei einer von einem Punkt ausgehenden Verzweigung alle Wahrscheinlichkeiten der davon ausgehenden Zweige addiert, muss man auf 1 bzw. 100 % kommen. Dementsprechend muss die Wahrscheinlichkeit für den anderen Zweig hier 25 % sein, damit man in Summe auf 75 % + 25 % = 100 % kommt. Das entpricht der Knotenregel [siehe auch: https://de.serlo.org/mathe/189811/pfadregeln].

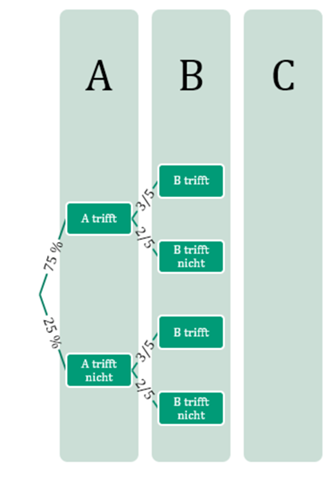
Nun hat man zwei Punkte in der Schicht „A“, von denen weitere Verzweigungen ausgehen, ob jeweils nun „B trifft“ oder „B trifft nicht“ eintritt. „B trifft“ hat eine Wahrscheinlichkeit von 3/5 (= 0,6 = 60 %). Die entsprechende Gegenwahrscheinlichkeit für „B trifft nicht“ ist 1 - 3/5 = 2/5 (= 0,4 = 40 %).

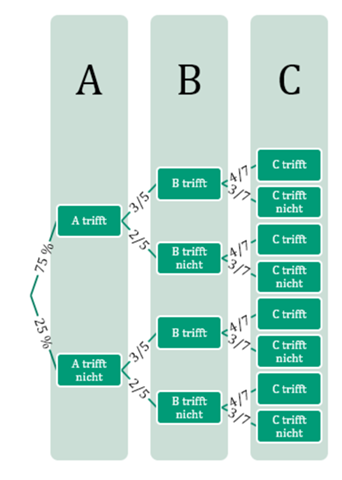
Genauso hat man dann von den Punkten in Schicht B ausgehend weitere Verzweigungen zu Schicht C.

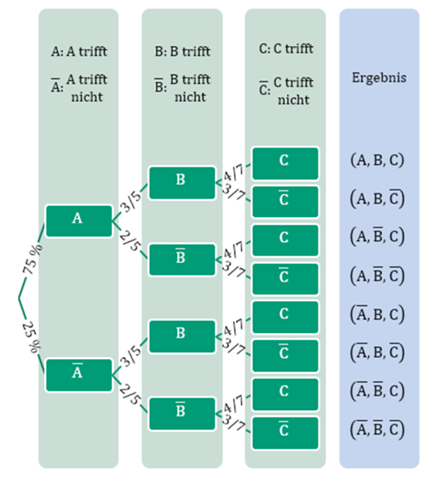
Damit man sich bei „A trifft“, „A trifft nicht“, etc. etwas Schreibarbeit spart, kann man das auch etwas abkürzen, indem man beispielsweise „A trifft“ kurz mit „A“ bezeichnet und „A trifft nicht“ mit „A̅“, etc.

Es gibt nun 8 verschiedene Endpunkte im Baumdiagramm. Jeder dieser Endpunkte entspricht einem Ergebnis. Die Wahrscheinlichkeit (vom Startpunkt ausgehend) dieses Ergebnis zu erreichen erhält man, indem man alle Einzelwahrscheinlichkeiten miteinander multipliziert, die man auffindet, wenn man vom Start bis zum entsprechenden Zielpunkt das Baumdiagram abläuft. Für das erste Ergebnis erhält man so beispielsweise die Wahrscheinlichkeit...

$P(\text{A}, \text{B}, \text{C})=75\,\%\cdot \frac{3}{5}\cdot \frac{4}{7}=\frac{3}{4}\cdot \frac{3}{5}\cdot \frac{4}{7}=\frac{3\cdot 3\cdot 4}{4\cdot 5\cdot 7}=\frac{36}{140}\approx 0\text{,}257=25\text{,}7\,\%$

Das entspricht der 1. Pfadregel (Produktregel). [Siehe auch: https://de.serlo.org/mathe/189811/pfadregeln]

Nun sollen gewisse Ereignisse betrachtet werden. Beispielsweise wird das Ereignis betrachtet, dass „alle drei Bälle im Tor liegen“ betrachtet. Nun schaut man, welche der Ergebnisse zu diesem Ereignis passen und summiert die entsprechenden Wahrscheinlichkeiten, um die Wahrscheinlichkeit des betrachteten Ergebnisses zu erhalten. Das entspricht der 2. Pfadregel (Summenregel). [Siehe auch: https://de.serlo.org/mathe/189811/pfadregeln]

Zum Ereignis, dass „alle drei Bälle im Tor liegen“, passt nur das Ergebnis (A, B, C) mit der Wahrscheinlichkeit 36/140, sodass man für die Wahrscheinlichkeit dieses Ereignisses...

$\frac{36}{140}\approx 25\text{,}7\,\%$

... erhält.

Zum Ereignis, dass „genau ein Ball im Tor liegt“ passen die Ergebnisse (A, nicht B, nicht C) und (nicht A, B, nicht C) und (nicht A, nicht B, C), sodass man für die Wahrscheinlichkeit dieses Ereignisses...

$\frac{18}{140}+\frac{9}{140}+\frac{8}{140}=\frac{18 + 9 + 8}{140}=\frac{35}{140}=0\text{,}25=25\,\%$

... erhält.

Zum Ereignis, dass „mindestens ein Ball im Tor liegt“ passen alle Ergebnisse außer dem Ergebnis (nicht A, nicht B, nicht C), sodass man...

$\frac{36}{140}+\frac{27}{140}+\frac{24}{140}+\frac{18}{140}+\frac{12}{140}+\frac{9}{140}+\frac{8}{140}=\frac{134}{140}\approx 0\text{,}957=95\text{,}7\,\%$

... oder alternativ auch...

$P(\text{„mindestens ein Treffer“})=1-P(\text{„kein Treffer“})=1-\frac{6}{140}=\frac{134}{140}\approx 0\text{,}957=95\text{,}7\,\%$

... für die Wahrscheinlichkeit dieses Ereignisses rechnen kann.

Answer 2

[rudirace]

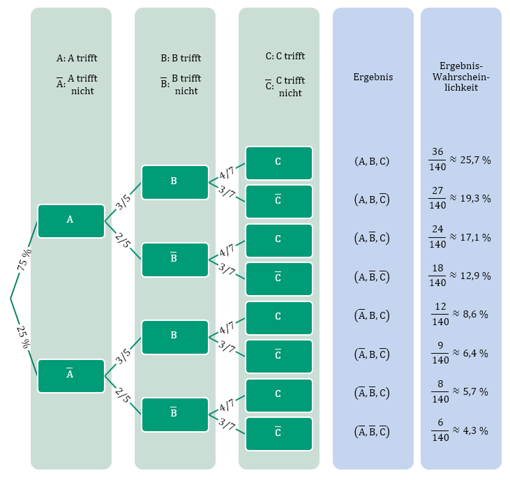
Das wäre mal ein Anfang für den Teil a)

Für b) und c) die anderen Zweige ergänzen und nachher rechts die Wahrscheinlichkeiten zusammenzählen

Woher ich das weiß: eigene Erfahrung

Comments

[Clarissa7567]

Also das wäre jetzt nur für A

wie wäre das für B

[rudirace]

@Clarissa7567

Du musst im Prinzip den ganzen Baum zeichnen. Also auch alle Wege, wenn der betreffende Stürmer nicht trifft. Es gibt nachher 8 verschiedene Wege. Entlang jedes Weges musst du die einzelnen Wahrscheinlichkeiten multiplizieren, um die Wahrscheinlichkeit für den gesamten Weg zu finden. Dann musst du alle Wege suchen, bei denen genau ein Stürmer trifft. Und die Wahrscheinlichkeiten für diese Wege addierst du dann.

[Clarissa7567]

@rudirace

Aber ich würde so sagen, dass man 1,2 und drei Möglichkeiten hat wegen diesen Aufgabenstellungen

[rudirace]

@Clarissa7567

Hmm, ich weiß nicht ganz was du meinst. Also bei Teil b) gibt es drei Möglichkeiten:

A triftt, aber B nicht und C auch nicht

A trifft nicht, B trifft und C trifft nicht

A und B treffen nicht aber C trifft

Also genau drei Wege, so dass nachher ein einziger Ball im Tor liegt.

[Clarissa7567]

@rudirace

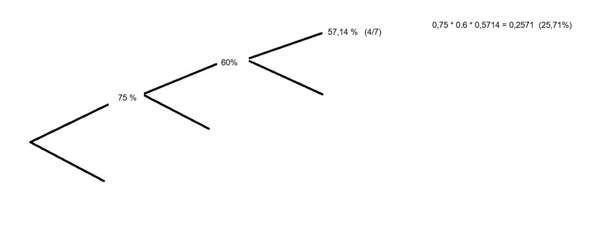
Könntest du mir das ganz kurz auf ein Blatt aufzeichnen weil ich komm nicht klar, mich verwirrt das Weil ich hab jetzt zum Beispiel ein Baumdiagramm gemacht mit 75 % 60 % und 57,14 % Wann hab ich an jeder Prozentzahl eine 1,2 und drei hingedacht aber das macht keinen Sinn

[rudirace]

@Clarissa7567

Ich kann das schon zeichnen, aber im Kommentar kann ich kein Bild einfügen. Oder ich weiß nicht wie das geht (Bild einfügen)...

[Clarissa7567]

@rudirace

Könntet du mir das privat schicken