Leitungsberechnung / maximale Kabellänge?
Hallo,
wenn ich ein Netzteil mit 12V/3A habe und mit 3 Verbrauchern (mit jeweils 20mA) belaste, wie lang darf das Kabel des Netzteils maximal sein bzw. wie weit darf der letzte Verbraucher vom Netzteil entfernt liegen? Alle Verbraucher liegen hintereinander auf dem selben Kabel.
Kabel: Kupfer, Querschnitt: 1,5 mm²
Welche Formel brauche ich hier bzw. wie sieht die Berechnung aus.
Danke vorab. .
3 Antworten
gehen wir mal davon aus, dass deine 3 verbraucher ganz am ende der leitung liegen, liegen sie über die leitung verteilt, dann wäre das ergebnis noch besser, d.h. es ginge mehr, aber wir bewegen uns hier auf grund der geringen ströme in bereichen, in denen das keinen siginifakten einfluss mehr hat.
die nächste frage wäre, wie weit die Spannung sinken darf, sprich wie viele von den 24 volt die verbraucher tatsächlich benötigen. gehen wir einfach mal von 5% aus, die wir runter können, das wären dann also 1,2 Volt, die uns am ende fehlen dürfen.
nach R = U / I hieße das bei einer spannungsdifferenz von 1,2 V und einem Strom von 0,06 A unser Widerstand darf 20 Ohm betragen.
für die berechnung des widerstandes einer leitung gilt R = l / q / A dabei steht l für die Länge in Metern, q für den Leitwert, bei Kupfer ist das die fixzahl 56 und A für den Querschnitt in mm²
umgestellt nach l lautet die formel L = q * A * R
den querschnitt kennen wir, das sind 0,8 mm² den Leitwert auch, das sind 56 und den Widerstand haben wir ja im ersten gang schon errechnet. das sind 20 Ohm.
Nach dieser Formel komme ich dann auf knapp 900 m bedenkt man, dass der strom ja nicht nur hin, sondern auch wieder zurück muss, bleiben noch maximal 450 m kabellänge über...
lg, Anna
mit der vorgabe hast du ja schon deine leitungslänge... dann kannst du die spannungsabfälle an den jeweiligen verbrauchern berechnen.
du rechnest also 100 m durch 56 durch 0,8 mm² um den Widerstand der ersten strecke zu ermitteln.
dann rechnest du nach U = R x I für deine 0,06 A den Spannungsabfall aus.
von diesem spannungswert aus, machst du das gleiche noch mal, diesmal aber mit 150 m und nur 0,04 A. und von dem ergebnis wiederum 150 m und 0,02 A
lg, Anna
Berechnung:
1. Verbraucher
L=100m q=56 A=0,08mm²
R=100m/56/0,08=22,32ohm
U1=22,32*0,06A=1,34V
2. Verbraucher
L=100m q=56 A=0,08mm²
R=150m/56/0,08=33,48ohm
U2=33,48*0,04A=1,34V
3. Verbraucher
L=150m q=56 A=0,08mm²
R=150m/56/0,08=33,48ohm
U3=33,48*0,02A=0,67V
Uges=U1+U2+U3=3,35V
24V-3,35V=20,65V <- Was am Ende bleibt.
Meinst du das so?
Ja, es ist ein Schreibfehler/Rechenfehler.
Berechnung:
1. Verbraucher
L=100m q=56 A=0,08mm²
R=100m/56/0,8=2,23ohm
U1=2,23*0,06A=0,13V
2. Verbraucher
L=150m q=56 A=0,08mm²
R=150m/56/0,8=3,35ohm
U2=3,35*0,04A=0,13V
3. Verbraucher
L=150m q=56 A=0,08mm²
R=150m/56/0,8=3,35ohm
U3=3,35*0,02A=0,067V
Uges=U1+U2+U3=0,33V
24V-0,33V=23,67V <- Was am Ende bleibt.
Wenn ich es nochmal durchrechne komme ich so auf nur rund 1,4% Spannungsverlust. Kann das sein?
Ich gehe mal von Gleichspannung und Parallelschaltung aus. Der Ersatzwiderstand der Verbraucher beträgt:
Rv = U : I = 24 V : 0,06 A = 400 Ω
Ein Spannungsfall sollte max. 3 % betragen. Somit ergibt sich ein maximaler Leitungswiderstand von 12,37 Ω (400 Ω : 97 % · 3 %). Die Grundformel für den Leitungswiderstand:
Rl = 2 · l : κ : q
umgestellt für die Berechnung der max. Länge:
l = Rl · κ · q : 2 = 12,37 Ω · 56 m/(Ω·mm²) · 0,8 mm² : 2 = 277,088 m
Ein Spannungsfall von 3% sind noch unbedenklich. Im Regelfall konnt ich mich immer auf diese App verlassen!
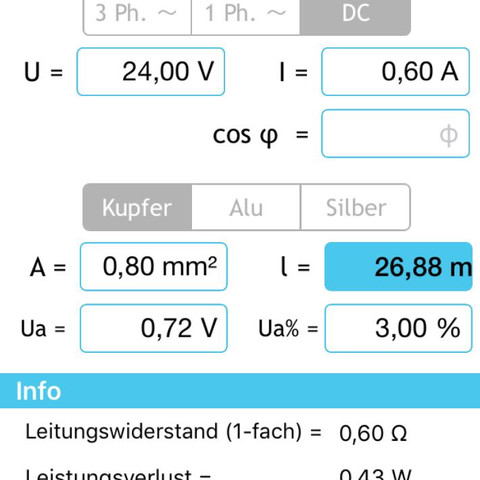
Vielen Dank. Wie würde das Ergebnis aussehen, wenn der Abstand zwischen den Verbrauchern 75 m betragen würde und der Abstand zwischen erster Verbraucher und Netzteil 50 m.