Kosmologische Expansion: Was genau ist rotverschoben?
Bei einem Doppler-ähnlichen Effekt (gern auch im expandierenden Raum) müsste doch das ganze Emissionsspektrum rotverschoben sein. Wenn es nur die Absorptionslinien der "Sternenatmosphären" sind, die sich relativ zum Emissionsspektrum verschieben, warum heißt es dann, dass die Lichtwellen der Galaxie gedehnt werden? Die Lücken im Spektrum entstehen doch dort vor Ort?
4 Antworten
... richtig, es ist das ganze Spektrum nach Rot, oder Blau, verschoben.
Alle verschiedenen Wellen werden gedehnt oder gestaucht, die Absobsionslinien der Elemente werden als Indikator benutzt.

Das kann man sich wiefolgt vorstellen:

Mit dem Doppler Effekt kann man das auch ausdrücken.

Auch die Gravitation kann eine Rotverschiebung verursachen.

mfe

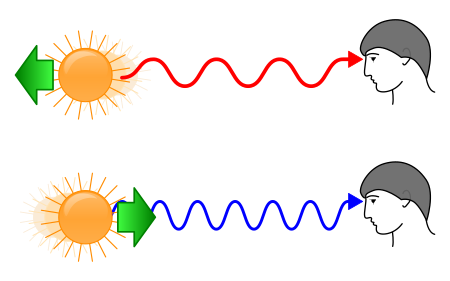
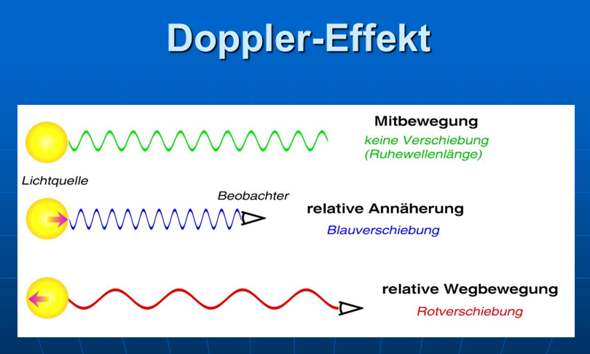
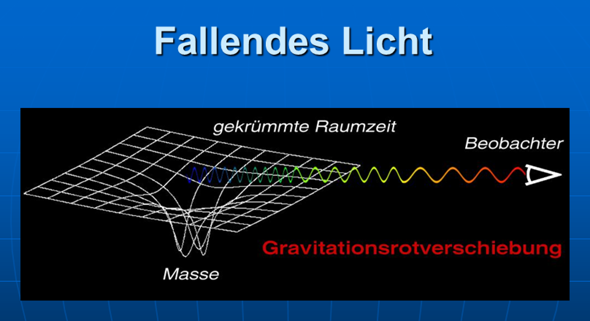
gerne.
das ganze Spektrum kann man nicht so messen das eine Verschiebung erkennbar wird, man braucht einen fixen Marker, die Absorptionslinien sind das...
alles verschiebt sich. Die Absorptionslinien sind nur eben die, deren Position im Spektrum man meistens misst.
Die Rotverschiebung der kosmologischen Expansion ist übrigens kein Dopplereffekt (sonst wäre z>1 nicht möglich). Die Wellenlängen werden einfach auf ihrem Weg zu uns zusammen mit dem Raum gedehnt.
(sonst wäre z>1 nicht möglich)
wieso sollte beim Doppler-effekt in einer flachen raumzeit durch relative bewegung keine rotverschiebung z>1 möglich sein?
1+z=lambda1/lambda2
Die Rotverschiebung der kosmologischen Expansion ist übrigens kein Dopplereffekt
man kann sicher koordinaten finden in denen man es so interpretieren kann (aber in diesen koordinaten wird das universum nicht homogen sein).
letztlich ist rotverschiebung durch kosmische expansion, gravitation und "klassischer" Doppler-effekt alles nur verschiedene spezialfälle ein und desselben allgemeinen prinzips.
weil dann v>c ?
nein. wieso?
(c=1)
lambda2 = lambda1*Wurzel((1+v)/(1-v))
1+z=lambda2/lambda1
und damit
1+z=Wurzel((1+v)/(1-v))
und damit
v=((1+z)²-1)/((1+z)²+1)
der nenner ist immer größer als der zähler, also ist immer v<1.
für z=1 hast du v=3/5, für z=2 hast du v=4/5, ...
ich kenne das so: 𝝺' = 𝝺(1 + v/c), für z > 1, also 𝝺' > 2𝝺 muss v/c > 1 sein. Wird auch hier so erklärt: https://www.leifiphysik.de/optik/wellenmodell-des-lichts/grundwissen/optischer-doppler-effekt
Wo ist der Fehler?
der fehler ist dass du nicht relativistisch rechnest. natürlich gibt es dann geschwindigkeiten v>c in der klassischen physik.
es ist immer gefährlich so etwas in einzelne teile aufzuspalten und klassisch zu denken. manchmal funktioniert es, manchmal fällt man damit auf die nase.
aber ja, der unterschied zwischen klassischer und relativistischer formel ist genau ein faktor Wurzel(1-v²), bzw bleibt für den transversalen Doppler-effekt (den es klassisch gar nicht gibt) nur dieser faktor. kann man vermutlich (meistens) wirklich so interpretieren.
das erinnert mich an relativistische kinetische Energie, aus der manche eine "relativistische Masse" herauslesen, die andere aber ablehnen, weil eigentlich nur die Ruhemasse die skalare ausschließliche Eigenschaft eines Objekts ist, die man als Masse kennt (eigentlich ist es ja eher eine richtungsabhängige Trägheit, die hier entsteht). Um der Eindeutigkeit von Begriffen willen wären neue Wörter für neue Begriffe vorzuziehen, was aber genau diese Aufspaltung in Teile fördert und dem Verstehen bzw Entstehen vereinigter Theorien im Wege steht. Vielleicht sollte man, wie in unserem Beispiel hier, auf die Begriffe Dopplereffekt und Zeitdilatation ganz verzichten und ganz neue Begriffe bilden, auf die man im Nachhinein die alten Begriffe als Speziallfälle mappt.
letztlich ist rotverschiebung durch kosmische expansion, gravitation und "klassischer" Doppler-effekt alles nur verschiedene spezialfälle ein und desselben allgemeinen prinzips
kommt denn bei der z-Berechnung für eine entfernte Galaxie das gleiche heraus, wenn ich den relativistischen Dopplereffekt beim Aussenden vergleiche mit der Integration der Expansion über die Zeit seit dem Aussenden?
kommt denn bei der z-Berechnung für eine entfernte Galaxie das gleiche heraus, wenn ich den relativistischen Dopplereffekt beim Aussenden vergleiche mit der Integration der Expansion über die Zeit seit dem Aussenden?
du meinst wenn du in obige formel ein "v" einsetzt und daraus die rotverschiebung ausrechnest? das kommt einzig auf die wahl der koordinaten an! es gibt in einer gekrümmten raumzeit keine eindeutige globale definition von räumlichem abstand und zeit. und damit hängt auch dein "v", definiert als die zeitliche änderung des abstandes, natürlich davon ab wie du das definierst.
in den üblichen FLRW koordinaten mit der (eigentlich willkürlichen) definition des räumlichen abstandes als proper distance at equal cosmic time kannst du nicht einfach so in die formel des "normalen" Dopplereffekts einsetzen. da kommt was falsches raus (siehst du ja schon daran dass uns auch signale von galaxien mit v>c erreichen, dann aber die wurzel imaginär wird).
aber man kann sicher koordinaten konstruieren in denen v genau so ist dass sich der korrekte wert für die rotverschiebung ergibt. hier geht dann eben am kosmischen ereignishorizont v->c. aber ich würde darin jetzt keinen vorteil oder tiefere erkenntnis sehen. wenn man die koordinaten so konstruiert dass genau das gilt, dann ist es natürlich keim wunder dass genau das gilt.
das allgemeine (koordinaten unabhängige) prinzip das immer und in jeder situation gilt um die rotverschiebung zu berechnen ist einfach das skalarprodukt der vierer-geschwindigkeit des empfängers bzw des senders mit dem vierer-wellenvektor des signals zu berechnen. alle bekannten formeln für den Dopplereffekt bzw rotverschiebung die man so findet sind einfach nur spezialfälle davon für bestimmte situationen.
Vielen Dank!
Hab meinen Denkfehler erkannt. Am sichtbaren Lichtspektrum ändert sich gar nichts, weil es vom UV her einfach nachrutscht (und Rot ins Infrarot verschwindet). Deshalb kann man die Verschiebung überhaupt nur an den Fraunhoferlinien sehen.
Der obligatorische Vergleich mit dem wegfahrenden Auto ist schuld. So kommt man auf die Idee, das Licht fliehender Galaxien müsste "röter" aussehen. Das gehört verboten - noch dazu wenn's gar kein Dopplereffekt ist... :)
Bei einem Doppler-ähnlichen Effekt (gern auch im expandierenden Raum) müsste doch das ganze Emissionsspektrum rotverschoben sein.
natürlich ist alles (jede elektromagnetische welle) rotverschoben.
Je weiter weg, desto schneller entfernt es sich, desto roter ist das Licht.
Vielen Dank, auch für die schönen instruktiven Bilder!
Ich glaub, ich hab meinen Denkfehler gefunden. Durch den beliebten Vergleich mit den Schallwellen denkt man, das Licht der fliehenden Galaxie müsste doch "röter" aussehen, so wie der Ton des wegfahrenden Autos tiefer wird. Aber das Licht (Spektrum unten im 1. Bild) bleibt identisch, weil die Wellenlängen vom UV her einfach nachrutschen. Deshalb kann man die Verschiebung tatsächlich nur an den Fraunhoferlinien erkennen. Indikator war das richtige Stichwort.