Knifflige Mathe-Aufgabe: Extrem schwer?
Hallo, kann mir jemand von euch bei dieser Mathe-Aufgabe helfen bzw. die Lösung sagen?
Maximilian bastelt für seine Schwester Theresa aus roten und schwarzen Perlen eine geschlossene Kette. Zwischen zwei gleichfarbige Perlen fügt er ein goldenes Zwischenstück ein, zwischen zwei verschiedenfarbige Perlen ein silbernes Zwischenstück. Theresa stellt fest, dass ihre Kette gleich viele goldene wie silberne Zwischenstücke hat. Zeige, dass die Anzahl der Perlen ein Vielfaches von 4 ist.
Ich wäre wirklich froh über Tipps oder Lösungen!
2 Antworten
Sei x die Anzahl der Wechsel von roten zu schwarzen Perlen. Da man bei einer geschlossenen Kette wieder bei der gleichen Farbe ankommt, gibt es ebenso viele Wechsel von schwarz nach rot, also ingesamt 2x Wechsel, also gibt es 2x Silberstücke. Laut Aufgabenstellung soll es ebenso viele Goldstücke geben, also insgesamt 4x Zwischenstücke, und damit auch 4x Perlen, die Anzahl ist also durch vier teilbar.
Die Lösung hängt von der Reihenfolge (Mischung der Perlen ab) Im Bild habe ich das skizziert. Ich komme nicht auf die gleiche Anzahl gold und silber.
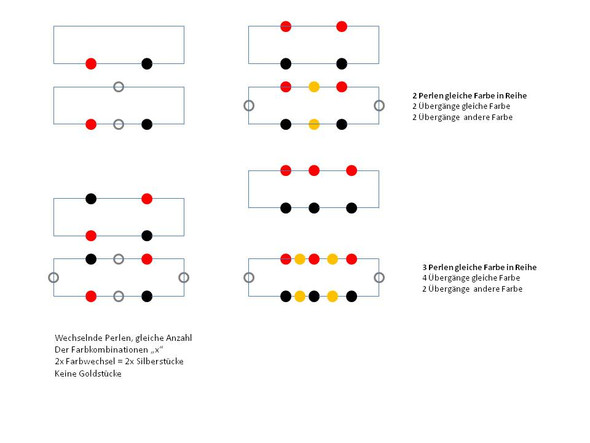
Es geht ja darum zu zeigen, dass die Anzahl durch 4 teilbar ist. wenn man weiß, dass es von jeder Sorte Zwischenstücke gleich viele gibt.
Dankeschön :-)