Ist der Graph der Funktion f(x)=e^x punktsymmetrisch zu f(x)=ln(x)?
Meine Frage: Ist der Graph der Funktion f(x)=e^x punktsymmetrisch zu f(x)=ln(x)? Wenn ja: wie lässt es sich beweisen? Wenn nein: Wie lässt es sich erklären? Dass eine Achsensymmetrie vorhanden ist ist klar... Danke schonmal, Grüße
5 Antworten
e^x und ln(x) sind nicht punktsymmetrisch.
Wäre nämlich Z = (a,b) der Spiegelpunkt (a>=0), dann müsste es zu e^(a+2a)=e^(3a) einen entsprechenden Spiegelpunkt auf ln(x) geben bei ln(a-2a) = ln(-a). Dies geht aber aus dem Definitionsbereich von ln heraus.
Für a<0 argumentierst du analog.
mE müssten die beiden Graphen bei Punktsymmetrie einen gemeinsamen Punkt haben; und das ist nicht der Fall. Sie spiegeln sich an einer Geraden und nicht an einem Punkt.
Schau dir meinen Kommentar zur Antwort von emaxba123 an. Es muss bei Punktsymmetrie keinen gemeinsamen Punkt geben, und die Achsensymmetrie schließt die Punktsymmetrie nicht aus.
Punktsymmetrie ist gegeben wenn:
f(-x) = -g(x)
Also müsste gelten:
e^(-x) = -ln(x).
Hey, lies dir doch einfach mal die Definition der Punktsymmetrie durch oder such mal, wie man punktsymmetrie beweisen kann (allgemein, nicht jetzt auf deine funktionen bezogen).
Deine Aufgabe löst sich dann von selbst - ist garnicht schwer !
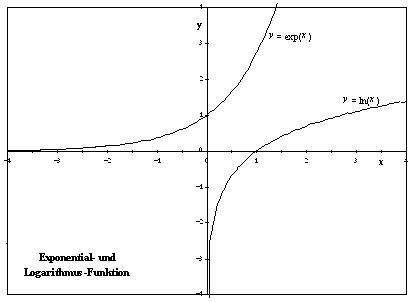
Mein Mathelehrer hat mich beauftragt das rauszufinden. Er hat gemeint dass es nicht punktsymmetrisch ist, er war sich aber wegen der Begründung nicht sicher, da wenn man das Bild anschaut auch eine Punktsymmetrie vermuten könnte. Deshalb Frage ich die Grage einfach anders: Warum ist er nicht Punktsymmetrisch?
Gespiegelt an der GERADEN y=x, da ln(x) Umkehrfunktion e^x ist.
Spiegle eine Gerade g an einem Punkt Z, der nicht auf g liegt. Du bekommst eine Parallele h. Nun ist h sowohl eine Punktspiegelung an Z von g als auch eine Achsenspiegelung an der Parallelen genau zwischen h und g. Zwei Figuren können also durchaus aus einer Punkt- und einer Achsenspiegelung auseinander hervorgehen.
Das gilt aber nur, wenn der Symmetriepunkt der Koordinatenursprung ist. Dies muss aber nicht zwngsläufig sein.