Ich brauche Hilfe bei Mathe?

Bei Aufgabe d) hab ich zwei Massen angegeben, mit denen ich das Volumen, den Oberflächeninhalt und die Mantelfläche eines quadratischen Pyramide berechnen muss. Um den Volumen zu berechnen brauch ich eine Körper Höhe und um die Körper Höhe zu bestimmen, muss den Satz des Pythaghoras anwenden, doch mein Ergebnis hat nicht mit der Lösung übereingestimmt.
Das Ergebnis meiner Lösung ist 29cm³.
Meine Rechnung 1:
Satz des Pythaghoras:
2,6² + 13² = hk²
6,76 + 169 = hk²
175,76 = hk² | wurzel ziehen
13,26 = hk
V = ⅓ × G × hk
V= ⅓ × 2,6 + 2,6 × 13,26
= 29,87cm³
Rechnung 2:
Satz des Pythaghoras
13² = 2,6² + hk²
169 = 6,76 + hk² | - 6,76
162,24 = hk² | wurzel ziehen
12,74 = hk
V = ⅓ × G × hk
= ⅓ × 2,6 × 2,6 × 12,74
= 28,71cm³
Was muss rauskommen, ich komme auf ein Volumen von 28,999
29cm³ muss rauskommen, dein ergebnis würde gelten. wie bist du drauf gekommen?
2 Antworten
Wo ist das rw.Dreieck aus a, hk und s?
Wenn hk die Höhe der Pyramide ist, auf der Skizze nur h:
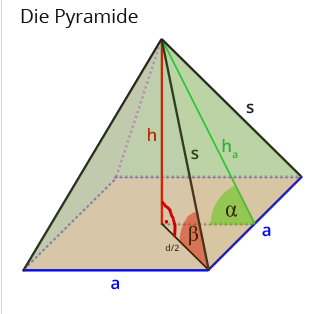
kann man nicht mit a rechnen, sondern mit der Hälfte der Diagonalen, Skizze d/2.
d/2, s und hk bilden ein rw. Dreieck.
Die Diagonale mit dem S.d.P. ausrechnen.
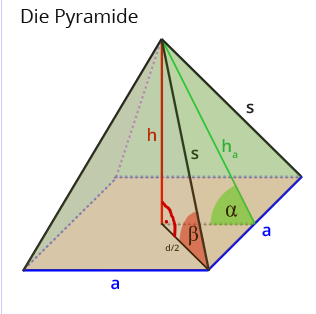
bei uns wird das anders genannt aber mit hk ist halt die höhe h gemeint
Ich komm auf folgendes Ergebnis.
Bei d muß man ja erst h ausrechnen für das Volumen.
Berechnung h (hk)
Gesucht: Körperhöhe h (hk)
Gegeben: a = 2,6 cm
Gegeben: s = 13 cm
---
h = Wurzel( s² - ( (Wurzel(2) * a) / 2 )² )
h = Wurzel( 13^2 - ( (Wurzel(2) * 2,6) / 2 )^2 )
Körperhöhe h (hk) beträgt 12,869343 cm
---------
Berechnung V
Gesucht: Volumen V
Gegeben: a = 2,6 cm
Gegeben: h = 12,869343 cm
---
V = (1/3) * a² * h
V = (1/3) * 2,6^2 * 12,869343
Volumen V beträgt 28,99892 cm³
die klammern verwirren mich ein bisschem...