Höhe eines Berges berechnen?
Ich habe bereits einen ziemlich umfangreichen Lösungsweg gefunden. Diese Person auf einem Forum hat es aber anders und mit kürzerem Weg gelöst.
Ich verstehe nicht wie sie für
b = a * 1 / 2√3 -3
aufstellt, wenn a = a. Woher kommt das im Nenner?
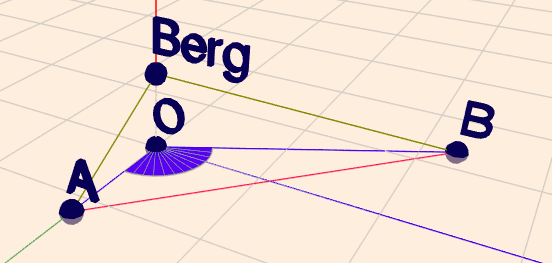
Von der Spitze eines Berges sieht man den Kirchturm in der Gemeinde A unter einem Tiefenwinkel 30 Grad und nach einem Schwenk des Fernrohrs um 120 Grad den Kirchturm der Gemeinde B unter einem Tiefenwinkel von 15 Grad.
Die beiden Türme stehen auf der selben Horizontalebene und sind 3,4 km voneinander entfernt.
Wie hoch ist der Berg?

1 Antwort
Ich lasse das a mal weg:
√3 / (6 - 3 * √3)
Im erste Schritt wurde √3 im Zähler und Nenner ausgeklammert und gekürzt:
1 / ((6 / √3) - 3)
Im zweiten Schritt wurde 6 / √3 der Nenner mit √3 erweitert:
1 / ((6 * √(3) / 3) - 3)
Im dritten Schritt wurde gekürzt:
1 / (2 * √(3) - 3)
tan(30°) = (1 / 3) * √3
Das wurde in der vierten Zeile eingesetzt. Dabei ist die 3 unter dem Bruchstrich direkt mit dem Nenner verrechnet worden.
Das entnimmt man einer Tabelle mit besonderen Funktionswerten oder man leitet es her:
In einem gleichseitigen Dreieck (α = β = γ = 60°) mit der Grundseite a und der Höhe h gilt laut Pythagoras:
h² = a² - (a / 2)²
h = (√(3) / 2) * a
Die Höhe h teilt das Dreieck in 2 kongruente Hälften mit dem Spitzenwinkel γ / 2 = 30°.
Es gilt laut Tangens:
tan(30°) = (a / 2) / h
tan(30°) = (a / 2) / ((√(3) / 2) * a)
tan(30°) = a * 2 / (2 * √(3) * a)
tan(30°) = 1 / √(3)
tan(30°) = √(3) /(√(3) * √(3))
tan(30°) = √(3) / 3
tan(30°) = (1 / 3) * √(3)
Dankeschön! Woher kommt die Wurzel aus 3 aber überhaupt?