Hilfe bei Thermodynamik?

Hallo, wie man die isobaren und isothermen Zustände ausrechnet weiß ich. Habe jetzt aber schwierigkeiten bei der isentropen ZÄ. Ich habe alle Zustände 1 gegeben, aber da p2, v2 und T2 unterschiedlich sind weiß ich nicht wie man das ausrechnen soll...
Könnte mir jemand erklären, wie man es dann ausrechnen soll und wie man eigentlich ein pv und Ts Diagramm zeichnet? Da habe ich leider auch noch schwierigkeiten...
Lösungen von meinem Prof:

Dankeschön für die Hilfe!
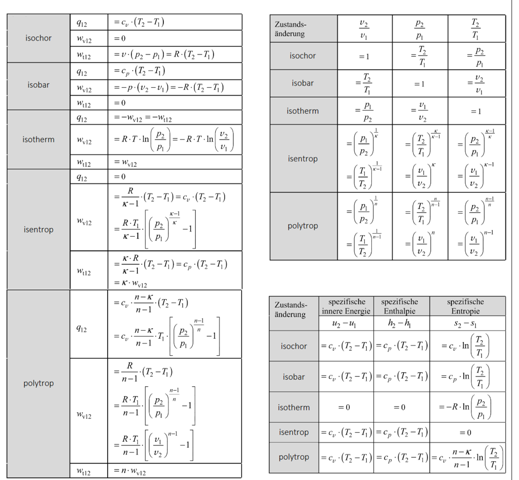
Zustandsänderungen idealer Gase
2 Antworten
Hier geht es offensichtlich um die sogenannten polytropen Zustandsänderungen von idealen Gasen.
Völlig unabhängig welche Zustandsänderung man hat, resultiert aus der idealen Gasgleichung die sogenannte Polytropengleichung. Diese lautet:
p * V^n = const.
und in ihrer spezifischen Form:
p * v^n = const.
n ist dabei der Polytropenexponent. Sämtliche Zustandsänderungen, also isotherm, isobar, isochor oder isentrop lassen sich durch die Wahl des Polytropenexponenten beschreiben. Dabei gilt:
isobar: n = 0 (V^0 = 1 und p * 1 = p...also bleibt p konstant)
isotherm: n = 1 (also p * V = const., welches das Gesetz von Boyle-Mariotte ergibt)
isentrop: n = κ
isochor: n = ∞
Reale technische Prozesse haben je nach Prozessführung unterschiedliche Polytropenexponenten irgendwo zwischen 0 und unendlich. Hat man für eine konkrete Anlage bzw. Prozessführung den Polytropenexponenten ermittelt, kann man damit auch ander Zustandsänderungen berechnen. Das ist dann aber was für Fortgeschrittene.
Mehr zu isentrop: n = κ
κ (kappa) ist der sogenannte Isentropenexponent. Es wird keine Entropie erzeugt oder abgegeben, die Entropie bleibt konstant, daher ist das isentrop. Eine isentrope Zustandsänderung ist immer adiabat und reversibel. Mit Wärme würde auch Entropie transportiert und bei einer nicht reversiblen Zustandsänderung würde Entropie erzeugt werden, Beides ließe die Entropie nicht konstant bleiben. Für den Isentropenexponent κ gilt:
κ = cp / cv
Für einatomige ideale Gase ist κ = 1,66
für zweiatomige Gase und damit auch Luft ist κ = 1,4
Entsprechend der Exponentialgleichung
p * V^n = const.
ergibt das im p-V-Diagramm dann unterschiedliche exponentielle Kurven:

Der Schnittpunkt der Kurven ist Zustand 1, der ja gegeben und daher gleich ist.
Isobar und isochor sind logischerweise Geraden parallel zu den Achsen.
isotherm mit n = 1 und daher mit p = const./V ergibt eine klassische Hyperbel.
bei einer adiabaten Verdichtung muss mit sinkendem Volumen der Druck stärker steigen als bei T = const., weil ja nicht gekühlt wird, sondern die Temperatur stark ansteigt, was gleichzeitig zu einem stärkeren Druckanstieg führt.
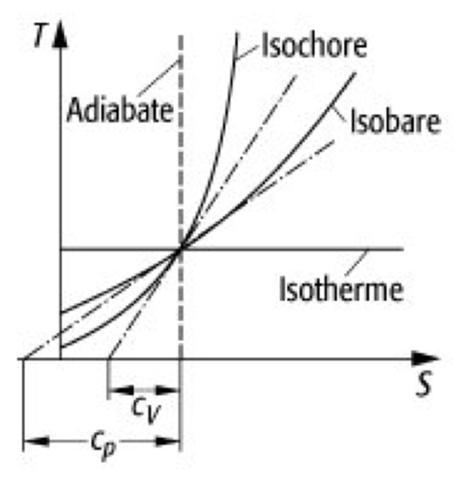
In einem T-s Diagramm sieht das dann so aus:

Adiabate (= Isentrope) und Isotherme müssen zwangsläufig konstante Geraden sein. Die Isobare ist nur leicht linksgekrümmt gegenüber einer Geraden.
Aus der Polytropengleichung, kombiniert mit dem idealen Gasgesetz, ergeben sich damit folgende Zusammenhänge:

Damit lassen sich dann die gesuchten Werte berechnen:
p2 = p1 * (V1 / V2)^n
Beispiel isentrop:
p2 = 0,2 MPa * (1/0,5)^1,4 = 0,53 MPa
Ergänzung zur Aufgabe c)
Da wir keine Angabe über die Masse oder das absolute Volumen haben, können wir im Weiteren nur mit den spezifischen Werten weiterrechnen, also mit q12.
Die Berechnung kann nach deiner Formelsammlung erfolgen. Dazu benötigt man aber die Werte für cv und cp.
Die können wir aber leicht berechnen. Aus der Formel für die isentrope Volumenänderungsarbeit folgt nach Kürzen der Klammer (T2 - T1):
cv = R / (κ - 1) = 288,3 J/kgK / 0,4 = 720,75 J/kgK
aus dem Zusammenhang:
κ = cp / cv ergibt sich:
cp = cv * κ = 720,75 J/kgK * 1,4 = 1009 J/kgK
Der Rest ist reine Fleißarbeit: abschreiben der Formeln und Werte einsetzen.

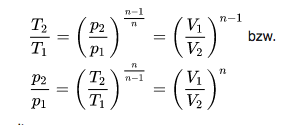
Ich habe mal einen Teil meiner Formelsammlung mal oben hochgeladen
Diese Formelsammlung ist genial, die hat mir gerade noch gefehlt. Gucke mir das morgen nochmal an.
Folgende Fragen hätte ich noch:
1.Ich habe diese Formel auch allerdings mit dem spezifischen Volumen v, aber V und kleines v ist ja nicht das gleiche? Trotzdem sehe ich sehr häufig das die leute einfach statt kleines v das große V nehmen zum beispiel beim idealen Gas gesetzt das lautet pv=RT und pV=RT gibt es nicht oder? Jetzt frage ich mich zum Beispiel ist die Formel die du rein geschrieben hast das Spezifische Volumen v oder das richtige Volumen V? Weil ich habe die selbe Formel bei mir stehen nur mit dem spezifischen Volumen v...
2.Woher weiß ich das mein Gas ein,zwei oder drei atomig ist? CO2 soll 3 haben aber Luft die wir in den Aufgaben nur als N2O2 betrachten nur 2? für mich wäre das 4 Atomig.
- Also kann man sich theoretisch auch einfach merken wie die isobaren,isothermen usw. in einem Diagram eingezeichet werden?
zum beispiel beim idealen Gas gesetzt das lautet pv=RT und pV=RT gibt es nicht oder?
So ist es. Entweder:
p * V = m * R * T oder mit m gekürzt:
p * v = R * T
Nun ist es aber bei einem Verhältnis
(V1 / V2) anders, sofern die Masse unverändert ist. Dann kann man schreiben:
V1 = v1 * m
V2 = v2 * m
Wenn man nun schreibt:
(V1 / V2) = (v1 * m / v2 * m)
kann man m rauskürzen und es ergibt sich, dass das Verhältnis des absoluten Volumens = dem Verhältnis des spezifischen Volumens ist:
(V1 / V2) = (v1 / v2)
Jetzt frage ich mich zum Beispiel ist die Formel die du rein geschrieben hast das Spezifische Volumen v oder das richtige Volumen V?
Wie gesagt, das ist Hose wie Jacke, da sich m rauskürzt. Manchmal gehts in der TD auch ganz einfach zu.
Woher weiß ich das mein Gas ein,zwei oder drei atomig ist? CO2 soll 3 haben aber Luft die wir in den Aufgaben nur als N2O2 betrachten nur 2? für mich wäre das 4 Atomig.
Das siehst du an der chemischen Formel:
CO2 hat 1 Kohlenstoff und 2 Sauerstoffatome, also besteht das Molekül aus 3 Atomen.
N2 besteht aus zwei Stickstoffatomen
O2 besteht aus zwei Sauerstoffatomen
N2O2
Was soll das sein? Distickstoffdioxid?? Wo soll es diese chemische Verbindung geben? In der Luft bestimmt nicht. Die besteht zu 78 % aus N2 und zu 21 % aus O2. Da sie also zu 99 % aus zweiatomigen Molekülen besteht, kann man sie in sehr guter Näherung insgesajmt als zweiatomige mit kappa = 1,4 annehmen. Das bischen Co2 und die paar einatomigen Edelgasmoleküle sowie weitere Spurengase machen da auch nicht viel aus (exakter Wert Luft: kappa = 1,404)
Also kann man sich theoretisch auch einfach merken wie die isobaren,isothermen usw. in einem Diagram eingezeichet werden?
Ja, da bleibt dir nichts anderes übrig, als das auswendig zu lernen und dir Merkhilfen durch die Logik zu schaffen.
1.Dann wäre H2,O2 und N2 auch alles zwei atomige Gase oder?
Sagen wir mal ich habe jetzt ein Gasgemisch das zu 80% aus CO2 besteht und 20% aus O2 wie wäre es in so einem Fall?
2.Wenn der Polytropenexponent undendlich ist kann man die Aufgabe dann eigentlich über die Polytropenformeln rechnen?
Hättest du eventuell noch ein Beispiel wo sich die Masse verändert? Bei idealen Gasen dürfte sich eigentlich ja wenn nur die Dichte oder das Volumen verändern oder?
Dann wäre H2,O2 und N2 auch alles zwei atomige Gase oder?
Genau.
Sagen wir mal ich habe jetzt ein Gasgemisch das zu 80% aus CO2 besteht und 20% aus O2 wie wäre es in so einem Fall?
Dann gibt es einen Isentropenexponenten zwischen 1,4 und 1,3.
Wenn der Polytropenexponent undendlich ist kann man die Aufgabe dann eigentlich über die Polytropenformeln rechnen?
Nein, deswegen wird das in deiner Aufgabe auch nicht gefordert.
Hättest du eventuell noch ein Beispiel wo sich die Masse verändert?
Nein, in einem geschlossenen System verändert sich keine Masse.
Okay verstehe, dann werde ich erstmal weiter probieren, das war mir wieder einmal eine sehr große Hilfe Dankeschön!
Im Endeffekt basiert das alles auf dem ersten Hauptsatz der Thermodynamik.
U = W + Q
Innere Energie = Volumenarbeit + Wärme
Funktioniert das mit dem Ansatz, bzw. kannst du mal deinen Rechenweg reinschicken?
Über die Polytrope Gleichung kann ich aber nicht die Wärmeenergie q12 ausrechnen. Was aber über die Isotherme ZÄ mit dem idealen Gas gesetzt funktioniert q12=-RT*ln(p2/p1). Soll man das dann einfach in Aufgaben Teil c über die isotherme ZÄ berechnen?