Frage zu Folge wächst höchstens so schnell wie?
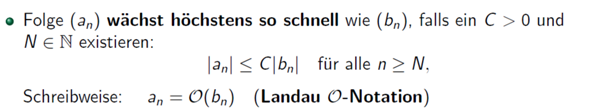
Was ich hier nicht kapiere, ich sage es muss ein C geben, wofür das gilt.
Wenn ich jetzt einfach zwei Folgen habe a_n und b_n und a_n wächst schneller als b_n, aber ich wähle jetzt als C einfach 10000000000000000000000
und b_n*C ist das wahrscheinlich größer als der Betrag von a_n, deshalb wächst doch b_n nicht schneller?
2 Antworten
Die Idee ist, dass wenn a_n "viel schneller" wächst als b_n, dass immer ein n geben wird, sodass a_n > C*b_n für alle C.
Wenn a_n allerdings nur höchstens so schnell wächst wie b_n, gibt es eben ein C, sodass a_n < C*b_n.
Z.B. gilt für f(x) = x + 10 und g(x) = x auch, dass f(x) > g(x) für alle x. Man kann aber ein C finden (z.B. C = 2), sodass f(x) < 2*g(x) für n > 11.
Wäre f(x) = e^x und g(x) = x würdest du zum Beispiel kein C finden.
Aber was heißt schneller wächst?
Wenn du kein C findest, sodass die obige Ungleichung erfüllt ist.
Wenn ich z. B. habe dass mein a_n gegen 1 konvergirt, aber extrem schnell, dagegen kovnergiert b_n sehr langsam, aber gegen 10, dann ist doch b_n größter, obwohl a_n langsamer konvergiert?
Mit Konvergenzgeschwindigkeit hat das alles jetzt noch nichts zu tun. Du sollst das "Langzeitverhalten" der Folgen für große n untersuchen. Konvergierende Folgen sind da eher langweilig, weil die haben eigentlich immer O(1), weil sie beschränkt sind.
Wenn ich jetzt einfach zwei Folgen habe a_n und b_n und a_n wächst schneller als b_n, aber ich wähle jetzt als C einfach 10000000000000000000000
und b_n*C ist das wahrscheinlich größer als der Betrag von a_n, deshalb wächst doch b_n nicht schneller?
Negiere Mal die Aussage:
Für alle C>0 und N aus N existiert ein n >=N sodass |a_n| > C|b_n|
Wenn also a_n schneller wächst als b_n, (also wächst a_n nicht höchstens so schnell wie b_n) ist es nicht möglich ein C und ein N zu finden sodass die Definition erfüllt ist. Da bringt es auch nichts, C riesig zu wählen, |a_n| wird trotzdem irgendwann größer.
Ein Einfaches Beispiel:
a_n = n
b_n = 1 für alle n
Dann wirst kein C und kein N finden, sodass
|a_n| <= C*|b_n| für alle n>= N gilt.
Das stimmt. aber wie kann ich das bei konvergierenden Folgen anwenden? WEnn ich eine Folge habe die gegen 1 kovnergeirt aber extrem schnell und dann eine Folge die gegen 10 konvergiert, jedoch sehr langsam, so find eich ein C für b_n, obwohl b_n langsamer wächst?
Aber was heißt schneller wächst? Wenn ich z. B. habe dass mein a_n gegen 1 konvergirt, aber extrem schnell, dagegen kovnergiert b_n sehr langsam, aber gegen 10, dann ist doch b_n größter, obwohl a_n langsamer konvergiert?