Energie an Blindelement?
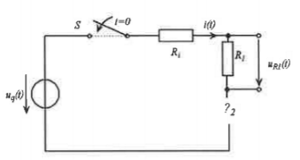
Folgende Bauteilwerte sind noch bekannt: Ri=90 Ohm, R1=60 Ohm, uq(t)=U0=150V
Die Energie der Quelle habe ich bereits wie folgt berechnet:
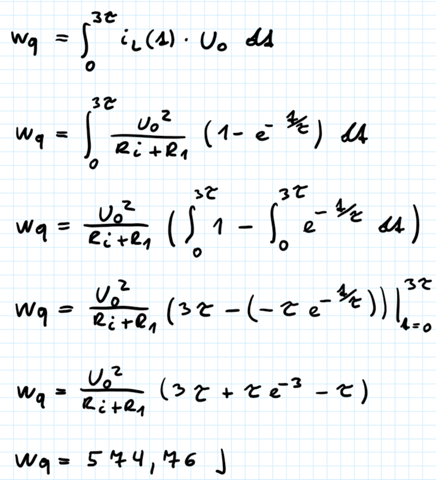
Nun zur Frage:
Gibt es eine elegante Möglichkeit (ohne Integration) durch die Quellenergie auf die Energie in der Spule zu schließen? Nochmal integrieren ist ja ziemlich langweilig ;D
2 Antworten
Hier muss man zwar theoretisch integrieren, aber man kann auch die gespeicherte Energie in einer Spule als bekannt voraussetzen, da dies eine bekannte Gleichung ist:
>Sind 0,12658J für die Energie in der Spule plausibel? Immerhin liefert die Quelle ja ganze 574,76J. Hab ich einen Fehler gemacht?
Die Energie der Quelle ist aber nicht 574J, sondern eher ein Tausendstel davon. Wo ist also dein kleiner Fehler?
Danke :) Hab beim Tau mit ms gerechnet, anstatt mit Sekunden :)
An der Integration führt eigentlich kein Weg vorbei, weil der Einschaltstrom der Exponentialfunktion folgt.
Nur für den Fall, dass die Einschaltdauer klein im Vergleich zur Zeitkonstante ist. Oder anders betrachtet: Wenn Du eine grosse Zeitkonstante im Vergleich zur Einschaltdauer hast, dann darf der Term
1 - e^(-t/T)
durch den linearen Term
t/T
ersetzt werden. Der Strom steigt dann näherungsweise linear mit der Zeit, womit dann nur noch die Fläche unter einem Dreieck zu berechnen wäre. Das geht ohne Integral.
Plausibel ist der Wert schon. Nach 3T hat die Spule 95% ihres Maximalstromes erreicht. Der Maximalstrom beträgt 150V / 150ohm = 1A. Dann beträgt die gespeicherte Energie überschlagsmässig 280,4/2 mJ ~ 140 mJ. Deine Rechnung passt somit. Der weit überwiegende Teil der Energie wird eben in den Widerständen "verbrannt".
>Der weit überwiegende Teil der Energie wird eben in den Widerständen "verbrannt".
Die maximal mögliche Leistung der Quelle sind 1A*150V = 150W. In den drei Zeitkonstanten, d.h. in 5.6ms, kann daher maximal 150W*5.6ms = 0,84J aus der Quelle herauskommen. 574J können daher nicht stimmen. Nehmen wir 0,574J, sieht das viel besser aus ;-)
Sehr wahrscheinlich hast Du für tau den Wert 1.87 und nicht 0.00187 eingesetzt.
Anmerkung: Fläche unter einem Dreieck ist auch ein Integral, eben von einer linearen Funktion
Kurze Frage noch:
Meine Integration ergab folgende Formel:
w_L=L/2*i_L^2(t) für t=0 bis t=3T
Mit den Zahlenwerten eingesetzt ergeben sich für die Energie in der Spule 0,12658J.
Sind 0,12658J für die Energie in der Spule plausibel? Immerhin liefert die Quelle ja ganze 574,76J. Hab ich einen Fehler gemacht?