Volumenintegral komplizierte Fragen?
Beim Wegintegral berechnet man einen Komplizierten Weg aus oo einfachen Wegen und beim Volumenintegral die Masse aus oo Massenpunkten, oder?
Zuerst eine Frage zum Wegintegral. Was heißt, über den Weg C integrieren? Sind dann r1 und r2 einfach die obere und untere Grenze?
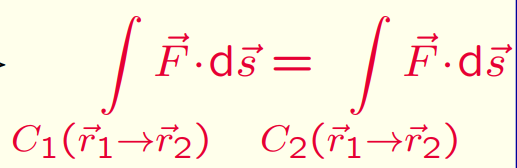
Und noch eine zum Volumenintegral. Die Formel für das Massenelement ist ja rho(ri)*V(ri). Wieso ist das in der Integration eine andere Formel? Wieso ist da die Formel rho* Funktion*V?
Allerdings, bei einer Integration von z.B. (2*x+4) dx wird ja das dx nicht mitgerechnet, sondern heißt nur, dass x die Variable ist. Heißt das dann, dass dV auch nicht mitgerechnet wird? Aber ich dachte, die Masse ist rho *V?
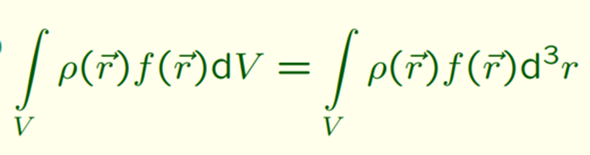
Und hier gibt es beim el. Feld auch sowas. Das ist auch ein Volumenintegral. Also wenn man statt der normalen Dichte die Ladungsdichte nimmt, kommt statt m Q raus, oder? Und für das el. Feld wird rho einfach nur mit der Punktladungsformel multipliziert, oder? Wieso genau? Und da steht d^3R. Heißt das, man soll die Integration dreimal mit den x, y, z-Kordinate von R machen, und dann multiplizieren?

Darf ich fragen, in welcher Ausbildung du dich befindest?
Im Biologiestudium mit Experimentalphysik als Nebenfach
Herzlichen Danke! Hattest du in der Oberstufe auch Physik?
Nein, ich hatte es nach der 10. abgewählt... Wobei ich sagen muss, das einzige, was ich von der Schule nicht vergessen hatte, war E h=mgh und E kin=1/2mv^2 :'-)
2 Antworten
Zuerst eine Frage zum Wegintegral. Was heißt, über den Weg C integrieren?
Soviel wie "entlang des Weges". Und wenn der Weg gekrümmt ist, dann eben "entlang des gekrümmten Weges"
Sind dann r1 und r2 einfach die obere und untere Grenze?
Im Prinzip ja, aber als Vektoren. Und nur wenn das Feld/Kraftfeld "konservativ" ist, spielt der Weg keine Rolle (und es existiert ein Potential des Kraftfelds)
Heißt das dann, dass dV auch nicht mitgerechnet wird?
Was heiß hier "nicht mitgerechnet"? "dV" ist das "infinitesimale" Volumenelement, die alle mit Hilfe der Integralrechnung "zusammengezählt" werden.
Aber ich dachte, die Masse ist rho *V
Fast nichts in dieser Welt ist so wie in der Schule konstant (außer Naturkonstanten natürlich). Alles hängt vom Ort ab und so ist auch die Dichte (ob von Masse oder Ladung) in der Regel nicht konstant. Die Dichte der Erde beispielsweise ist extrem inhomogen und daher ist die Dichte ρ selbst eine Funktion des Ortes und damit ρ(r) (Dichtefunktion der Masse). Im Ergebnis muss man eine Masse als Volumenintegral
berechnen (und dazu die Dichteverteilungsfunktion ρ(r) kennen) und nur wenn ρ(r) = ρ = konstant ist, kann man das ρ vor das Integral ziehen (Faktorregel) und damit wird die Masse mit
zu der Formel, die man in der Schule benutzt (in der man ja in aller Regel nur mit absolut idealisierten Systemen/Fällen rechnet)
R1 und R2 sind die Endpunkte des Weges. Das was hier steht bedeutet dass in einem konservativen Kraftfeld die Arbeit lediglich von den Endpunkten des Weges abhängt nicht aber von dem Weg welchen man wählt.
Das ist auch genau der Grund warum sich konservative Kraftfelder durch Potentiale beschreiben lassen.
Allerdings, bei einer Integration von z.B. (2*x+4) dx wird ja das dx nicht mitgerechnet, sondern heißt nur, dass x die Variable ist.
Das ist eine falsche Sicht. Das dx wird eingerechnet und ist ein Infinitisimal kleines Element in x Richtung.
dV ist ein Infinitismal kleines Volumen.
rho*f*dV bedeutet also man nimmt die Dichte irgendeine Funktion f und das Volumenselement dV und integriert dieses. Dadurch wird vereinfacht gesagt aus dV wieder V. Ich denke dieser Punkt solll aber nur das Volumensintegral allgemein beschreiben unter anderem wird hier auch die Bedeutung von d3 sichtbar. d3 ist vermutlich die Kurzschreibweise für dxdydz
Das was bei der Ladung steht bedeutet einfach nur wenn ich über eine Ladungsdichte integriere bekomme ich eine Ladung ist auch irgendwie klar. Wenn ich in einem Volumen n Elektronen habe dann hat das Volumen als ganzes die Ladung n*e, viel mehr bedeutet das Integral nicht.
Für das Elektrische Feld wird quasi einfach nur über Punktladungen in einem Volumen integriert. Das kannst du aufgrund des Superpositionsprinzips am Ende auch so machen, solange das Medium in welchem man rechnet Linear ist.