Dreiecksberechnung?
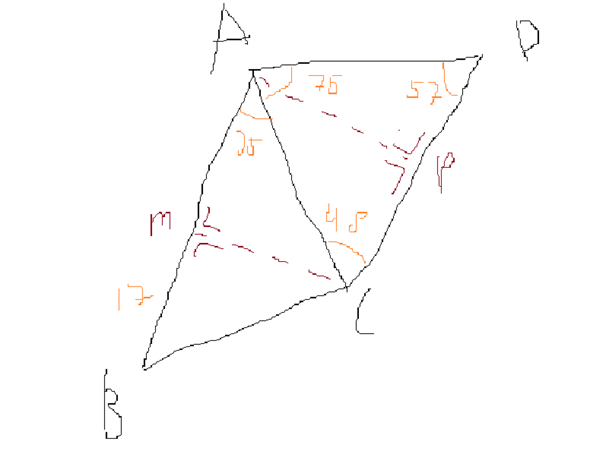
ich habe zwei "zusammenhängende" Dreiecke mit den Eckpunkten A B C D (siehe Anhang)
Vorgegeben sind beim:
Dreieck "1" die Seitenlänge von A:B mit 17 cm, der Winkel beim Eckpunkt A mit 35 und die Fläche von 54 cm2
Dreieck "2" die Winkel beim Eckpunkt C mit 48 und beim Eckpunkt D mit 57.
Gefragt ist die Fläche von Dreieck "2".
Bitte kann mir jemand "laienverständlich" die Berechnungsschritte erklären ?
Danke !

2 Antworten

1/2 * ML * 17 = 54 cm²
ML * 8,5 = 54
=> ML = 54/8,5
(Die Formel um ein Dreieck Oberfläche zu berechnen ist ein halb Viereck, also 1/2 * Länge * Breite. Jetzt ist ML die Länge und AB(17) die Breite. )
(wir wollen Länge ML weil wir mit die Sinus Regel Länge AC können berechnen und so was weiter bis AP und CD)
AC /sin90 = ML / sin35
AC/sin 90 = (54/8,5 ) / sin 35
=> AC = ((54/8,5)* sin90)/ sin 35 = 11,076
AP/ sin38 = AC /sin90
AP/ sin48 = 11,076/sin90
=> AP = 8,231
CD/ sin76 = AC /sin 57
CD/ sin75 = 11,076/sin57
=> CD 12,76
Erck ACD= 1/2 *CD * AP
Erck ACD= 1/2* 12,76*8,231
Erck ACD= 52,5 cm²
Mogentlich sind mein Sinus berechnungen nicht super deutlicht. Unten sehst du ein Beispiel, wie es auf dem Papier aussieht.

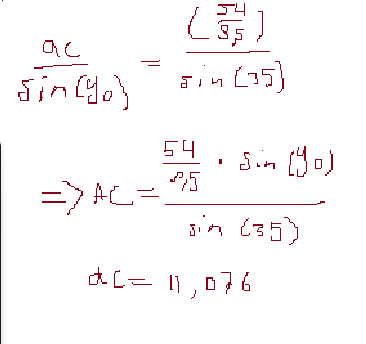
Der Flächeninhalt des Dreiecks ABC ist
1/2 * AB * AC * sin(35°)
Damit kann man die Länge AC ausrechnen.
Den Winkel CAD (75°) findet man über die Innenwinkelsumme im Dreieck ACD.
Die Strecke AD berechnet man mit dem Sinussatz.
Dann ist der Flächeninhalt des Dreiecks ACD
1/2 * AC * AD * sin(75°)
können Sie mir bitte eine Detailberechnung nachliefern - ich kann's einfach nicht (habe wohl bei Corona zu viel "verschlafen")