Dreiecks Konstruktion mit Winkelhalbierenden?
Also Folgende Informationen sind angegeben :
Winkelhalbierende Beta : 3 cm lang
Beta : 120 Grad
Gamma : 25 Grad
Wie gehe ich jetzt bei der Konstruktion vor? Ich verstehe das leider nicht...
2 Antworten
Hallo,
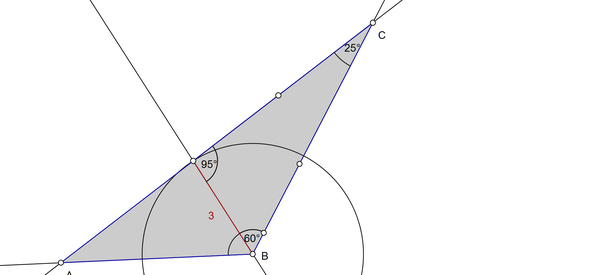
Du beginnst mit dem Winkel Beta, seinen beiden Schenkeln (Länge noch ungewiß) und dem Scheitel B. Bei B legst Du die Winkelhalbierende an, deren Länge Du kennst (3 cm). Der Winkel oberhalb der Winkelhalbierenden, also Beta/2, hat 60°. Gamma hat 25°, bleiben für den letzten Winkel am Ende der Winkelhalbierenden, dessen einer Schenkel die Halbierende ist und der andere Richtung Punkt C geht, 95°. Du trägst also diesen Winkel am anderen Ende der Winkelhalbierenden ab. Wo sich sein Schenkel und der Schenkel von Beta, der in Richtung Punkt C geht, schneiden, ist Punkt C.
Der Schnittpunkt in der anderen Richtung mit dem unteren SChenkel von Beta ist schließlich A und damit ist das Dreieck fertig.
Herzliche Grüße,
Willy
na ja... allerdings hat er solche in seinem BUch sicherlich :D irgendwann wurde es ja mal erklärt .aber nun habe ich sowie Du es noch mal erklärt und nun sollte er es kapiert haben :D
Leider eine Hausaufgabenfrage...
zur Not frag mal deine Kammeraden?
Nur soviel.... wenn Beta 120 und Gamma 25 Grad hat.. was hat Alpha?
Wenn die Winkel an den Ecken bekannt sind und die Winkelhalbierene auch ist auch der Winkel bekannt der am Ende der 3 cm halbierenden ist
Ich kenne ja alle Winkel, ( Alpha ist dann 35 Grad) Bloß wie finde ich heraus wie lang die seiten a,b,c sind
Brauchst du doch nicht .. Wenn du konstruierst (geometrisch) da du die Länge der Winkelhalbierenden und den Winkel hast 60 35 und Rest. Kannst du an der Liebe einen Winkel abnehmen und eine lienie zeichnen. Der Schnittpunkt mit der anderen ergibt die Länge ...
Vielen Dank! Habs jetzt verstanden :D